Discrete Fourier Transform (numpy.fft)¶
Standard FFTs¶
fft（a [，n，axis，norm]） |
计算一维离散傅里叶变换。 |
ifft（a [，n，axis，norm]） |
计算一维离散傅里叶逆变换。 |
fft2（a [，s，axes，norm]） |
计算2维离散傅里叶变换 |
ifft2（a [，s，axes，norm]） |
计算二维离散傅里叶逆变换。 |
fftn（a [，s，axes，norm]） |
计算N维离散傅里叶变换。 |
ifftn（a [，s，axes，norm]） |
计算N维离散傅里叶逆变换。 |
Real FFTs¶
rfft（a [，n，axis，norm]） |
计算实数输入的一维离散傅里叶变换。 |
irfft（a [，n，axis，norm]） |
计算实数输入的n点DFT的逆。 |
rfft2（a [，s，axes，norm]） |
计算实数组的二维FFT。 |
irfft2（a [，s，axes，norm]） |
计算实数组的二维逆FFT。 |
rfftn（a [，s，axes，norm]） |
计算实际输入的N维离散傅里叶变换。 |
irfftn（a [，s，axes，norm]） |
计算实际输入的N维FFT的逆。 |
Hermitian FFTs¶
hfft（a [，n，axis，norm]） |
计算具有厄密对称（实际频谱）的信号的FFT。 |
ihfft（a [，n，axis，norm]） |
计算具有厄密对称性的信号的逆FFT。 |
Helper routines¶
fftfreq（n [，d]） |
返回离散傅里叶变换采样频率。 |
rfftfreq（n [，d]） |
返回离散傅立叶变换采样频率（用于rfft，irfft）。 |
fftshift（x [，axes]） |
将零频率分量移动到频谱的中心。 |
ifftshift（x [，axes]） |
fftshift的逆。 |
Background information¶
傅里叶分析基本上是用于表示作为周期分量的和的函数，以及用于从那些分量恢复函数的方法。当函数和其傅里叶变换都用离散对等项代替时，它被称为离散傅里叶变换（DFT）。DFT已经成为数值计算的主要部分，这部分是因为用于计算它的非常快速的算法，称为快速傅立叶变换（FFT），其已知为高斯（1805），并且由Cooley和其当前形式Tukey [CT]。Press et al。[NR]提供对傅立叶分析及其应用的可访问介绍。
Because the discrete Fourier transform separates its input into components that contribute at discrete frequencies, it has a great number of applications in digital signal processing, e.g., for filtering, and in this context the discretized input to the transform is customarily referred to as a signal, which exists in the time domain. 输出称为频谱或变换，并存在于频域中。
Implementation details¶
有许多方法来定义DFT，在指数的符号，规范化等方面变化。在该实现中，DFT被定义为
DFT通常为复数输入和输出定义，并且线性频率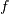
处的单频分量由复指数
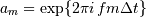表示，其中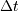
是采样间隔。
结果中的值遵循所谓的“标准”顺序：如果A = fft（a， n） ，则A[0]包含零频率项（信号的和），其对于实数输入始终是真实的。那么A[1:n/2]包含正频率项，而A[n/2+1:]降低负频率。对于偶数个输入点，A[n/2]表示正和负奈奎斯特频率，并且对于实际输入也是纯实数。对于奇数个输入点，A[(n-1)/2]包含最大的正频率，而A[(n+1)/2]例程np.fft.fftfreq(n)返回一个数组，给出输出中相应元素的频率。例程np.fft.fftshift(A)移动变换及其频率以将零频率分量置于中间，并且np.fft.ifftshift(A)撤消那个转变。
When the input a is a time-domain signal and A = fft(a), np.abs(A) is its amplitude spectrum and np.abs(A)**2 is its power spectrum. 相位谱通过np.angle(A)获得。
逆DFT定义为
它不同于正向变换的指数参数的符号和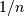
的默认归一化。
Normalization¶
默认归一化具有未缩放的直接变换，并且逆变换由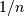缩放。通过将关键字参数norm设置为"ortho"（默认为None），可以获得酉变换，将缩放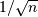
。
Real and Hermitian transforms¶
当输入是纯实数时，其变换是Hermitian，即，频率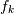
的分量是频率
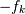处的分量的复共轭，这意味着对于实际输入，在负频率中没有信息从正频率分量中不可用的分量。系列的rfft功能设计为对实际输入进行操作，并通过只计算正频率分量，直到并包括奈奎斯特频率来利用这种对称性。因此，n输入点产生n/2+1复数输出点。该族的反相假设其输入的相同对称性，并且对于n点的输出使用n/2+1输入点。
相应地，当频谱是纯实数时，信号是厄密共轭。hfft系列通过在输入（时间）域中使用n真实点的n/2+1复杂点来利用这种对称性频域。
在较高维度中，使用FFT，例如用于图像分析和滤波。FFT的计算效率意味着它也可以是使用在时域中的卷积等价于频域中的逐点乘法的性质来计算大卷积的更快的方式。
References¶
| [CT] | Cooley，James W.和John W. Tukey，1965，“An algorithm for the machine calculation of complex Fourier series，”计算。19：297-301。 |
| [NR] | Press, W., Teukolsky, S., Vetterline, W.T., and Flannery, B.P., 2007, Numerical Recipes: The Art of Scientific Computing, ch. 12-13。剑桥大学Press，Cambridge，UK。 |
Examples¶
例如，参见各种功能。