numpy.fft.fftn

numpy.fft.fftn(a, s=None, axes=None, norm=None)

计算N维离散傅里叶变换。

该函数通过快速傅里叶变换（FFT）计算M t>维数组中任何数量的轴上的N离散傅里叶变换。

参数：

a：array_like

输入数组，可以复杂。

s：ints序列，可选

输出（s [0]指代轴0，s [1]到轴1等）的形状（每个变换轴的长度）。这对于fft（x，n）对应于n。沿任何轴，如果给定的形状小于输入的形状，则输入被裁剪。如果它较大，输入将用零填充。如果未给出s，则使用沿轴指定的轴的输入形状。

axes：ints序列，可选

计算FFT的轴。如果未给出，则使用最后的len(s)轴，如果s也未指定，则使用所有轴。轴中的重复索引表示该轴上的变换执行多次。

norm：{None，“ortho”}，可选

版本1.10.0中的新功能。

规范化模式（参见numpy.fft）。默认值为None。

返回：

out：complex ndarray

沿着轴指示的轴或者通过s和a的组合变换的截断或补零输入，如参数部分。

上升：

ValueError

如果s和轴具有不同的长度。

IndexError

如果axes的元素大于a的轴数。

也可以看看

numpy.fft

离散傅立叶变换的总体视图，使用定义和约定。

ifftn

fftn的逆，逆n维FFT。

fft

一维FFT，使用定义和约定。

rfftn

实输入的n维FFT。

fft2

二维FFT。

fftshift

将零频率项转移到数组的中心

笔记

类似于fft的输出包含所有轴的低阶角中的零频率项，所有轴的前半部分中的正频率项，所有轴中的奈奎斯特频率的项所有轴的中间和所有轴的后半部分中的负频率项，以负频率的减小的顺序。

有关详细信息，定义和使用的约定，请参见numpy.fft。

例子

>>> a = np.mgrid[:3, :3, :3][0]
>>> np.fft.fftn(a, axes=(1, 2))
array([[[  0.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j]],
       [[  9.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j]],
       [[ 18.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j],
        [  0.+0.j,   0.+0.j,   0.+0.j]]])
>>> np.fft.fftn(a, (2, 2), axes=(0, 1))
array([[[ 2.+0.j,  2.+0.j,  2.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j]],
       [[-2.+0.j, -2.+0.j, -2.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j]]])

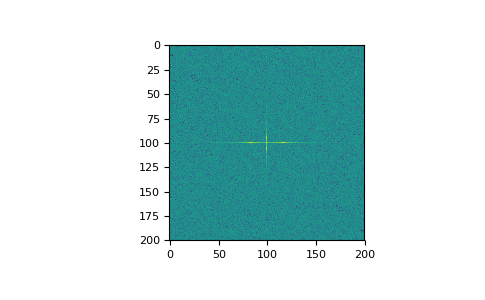
>>> import matplotlib.pyplot as plt
>>> [X, Y] = np.meshgrid(2 * np.pi * np.arange(200) / 12,
...                      2 * np.pi * np.arange(200) / 34)
>>> S = np.sin(X) + np.cos(Y) + np.random.uniform(0, 1, X.shape)
>>> FS = np.fft.fftn(S)
>>> plt.imshow(np.log(np.abs(np.fft.fftshift(FS))**2))
<matplotlib.image.AxesImage object at 0x...>
>>> plt.show()

（源代码，png，pdf）