numpy.polyfit

numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)

最小二乘多项式拟合。

拟合多项式p（x） = p [0] * x **度 + ... + p [deg] > deg到点（x，y）。返回使平方误差最小的系数p的向量。

参数：

x：array_like，shape（M，）

M个采样点（x [i]， y [i]）的x坐标。

y：array_like，shape（M，）或（M，K）

y坐标。通过传递每列包含一个数据集的2D阵列，可以一次拟合共享相同x坐标的样本点的若干数据集。

deg：int

拟合多项式的维度

rcond：float，可选

相对条件编号。相对于最大奇异值小于该值的奇异值将被忽略。默认值为len（x）* eps，其中eps是float类型的相对精度，在大多数情况下约为2e-16。

full：bool，可选

开关确定返回值的性质。当它为False（默认值）时，只返回系数，当来自奇异值分解的True诊断信息也返回时。

w：array_like，shape（M，），可选

应用于采样点的y坐标的权重。对于高斯不确定性，使用1 / sigma（不是1 / sigma ** 2）。

cov：bool，可选

返回估计和估计的协方差矩阵如果full为True，则不返回cov。

返回：

p：ndarray，shape（M，）或（M，K）

多项式系数，最高功率先。如果y是2-D，则k数据集的系数在p[:,k]中。

残差，秩，奇异值，rcond：

仅在full = True时存在。最小二乘拟合的残差，缩放的Vandermonde系数矩阵的有效秩，其奇异值和rcond的指定值。有关详细信息，请参阅linalg.lstsq。

V : ndarray, shape (M,M) or (M,M,K)

仅当full = False且cov` = True时才显示。多项式系数估计的协方差矩阵。该矩阵的对角线是每个系数的方差估计。如果y是2-D数组，则第k个第t个数据集的协方差矩阵在V[:,:,k]

警告：

RankWarning

最小二乘法拟合中的系数矩阵的秩是不足的。只有在full = False时，才会发出警告。

警告可以通过关闭

>>> import warnings
>>> warnings.simplefilter('ignore', np.RankWarning)

也可以看看

polyval

计算多项式值。

linalg.lstsq

计算最小二乘拟合。

scipy.interpolate.UnivariateSpline

计算样条拟合。

笔记

该解最小化平方误差

在等式中：

x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0]
x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]

系数p的系数矩阵是Vandermonde矩阵。

polyfit在最小二乘拟合严重时发出RankWarning。这意味着最佳拟合由于数值误差而不能很好地定义。可以通过降低多项式次数或通过将x替换为x - x .mean()来改善结果。rcond参数也可以设置为小于其默认值，但是结果拟合可能是假的：包括来自小奇异值的贡献可以向结果添加数值噪声。

注意，当多项式的阶数较大或者采样点的间隔严重居中时，拟合多项式系数本身会受到不利的影响。在这些情况下，应始终检查配合的质量。当多项式拟合不令人满意时，样条可能是一个好的选择。

参考文献

[R58]

维基百科，“曲线拟合”，http://en.wikipedia.org/wiki/Curve_fitting

[R59]

维基百科，“多项式插值”，http://en.wikipedia.org/wiki/Polynomial_interpolation

例子

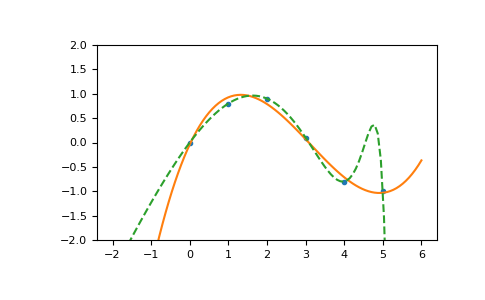
>>> x = np.array([0.0, 1.0, 2.0, 3.0,  4.0,  5.0])
>>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
>>> z = np.polyfit(x, y, 3)
>>> z
array([ 0.08703704, -0.81349206,  1.69312169, -0.03968254])

使用poly1d对象来处理多项式很方便：

>>> p = np.poly1d(z)
>>> p(0.5)
0.6143849206349179
>>> p(3.5)
-0.34732142857143039
>>> p(10)
22.579365079365115

高阶多项式可能会剧烈振荡：

>>> p30 = np.poly1d(np.polyfit(x, y, 30))
/... RankWarning: Polyfit may be poorly conditioned...
>>> p30(4)
-0.80000000000000204
>>> p30(5)
-0.99999999999999445
>>> p30(4.5)
-0.10547061179440398

插图：

>>> import matplotlib.pyplot as plt
>>> xp = np.linspace(-2, 6, 100)
>>> _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--')
>>> plt.ylim(-2,2)
(-2, 2)
>>> plt.show()

（源代码，png，pdf）