numpy.poly1d¶

class numpy.poly1d(c_or_r, r=0, variable=None)[source]¶

一维多项式类。

一个方便类，用于封装对多项式的“自然”操作，以便所述操作可以采用其在代码中的常规形式（参见示例）。

参数：	c_or_r：array_like 多项式的系数，以降低的功率，或者如果第二个参数的值为True，多项式的根（多项式计算结果为0的值）。例如，`poly1d（[1， 2， 3]）`返回表示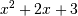 $x^2 + 2x + 3$ ，而`poly1d（[1， 2， 3]， True）`一个代表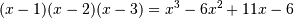 $(x-1)(x-2)(x-3) = x^3 - 6x^2 + 11x -6$ 。 r：bool，可选如果为真，则c_or_r指定多项式的根；默认值为False。 variable：str，可选更改将p从x更改为`variable`时使用的变量（请参阅示例）。

例子

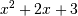构造多项式 $x^2 + 2x + 3$ ：

>>> p = np.poly1d([1, 2, 3])
>>> print(np.poly1d(p))
   2
1 x + 2 x + 3

评估 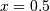$x = 0.5$ 处的多项式：

>>> p(0.5)
4.25

找到根：

>>> p.r
array([-1.+1.41421356j, -1.-1.41421356j])
>>> p(p.r)
array([ -4.44089210e-16+0.j,  -4.44089210e-16+0.j])

上一行中的这些数字表示（0,0）到机器精度

显示系数：

>>> p.c
array([1, 2, 3])

显示顺序（去除前导零系数）：

>>> p.order
2

显示多项式中的k次方的系数（相当于p.c[-(i+1)]）：

>>> p[1]
2

多项式可以加，减，乘和除（返回商和余数）：

>>> p * p
poly1d([ 1,  4, 10, 12,  9])

>>> (p**3 + 4) / p
(poly1d([  1.,   4.,  10.,  12.,   9.]), poly1d([ 4.]))

asarray(p)给出系数数组，因此多项式可以用于所有接受数组的函数：

>>> p**2 # square of polynomial
poly1d([ 1,  4, 10, 12,  9])

>>> np.square(p) # square of individual coefficients
array([1, 4, 9])

可以使用variable参数修改p的字符串表示中使用的变量：

>>> p = np.poly1d([1,2,3], variable='z')
>>> print(p)
   2
1 z + 2 z + 3

从它的根构造一个多项式：

>>> np.poly1d([1, 2], True)
poly1d([ 1, -3,  2])

这是与通过以下获得的相同的多项式：

>>> np.poly1d([1, -1]) * np.poly1d([1, -2])
poly1d([ 1, -3,  2])

属性

方法