numpy.random.hypergeometric¶

numpy.random.hypergeometric(ngood, nbad, nsample, size=None)¶

从超几何分布绘制样本。

样本是从具有指定参数的超几何分布绘制的，ngood（做出良好选择的方法），nbad（做出错误选择的方法）和nsample =抽样项目数，小于或等于总和ngood + nbad。

参数：	ngood：int或array_like 做出良好选择的方法数。必须为非负数。 nbad：int或array_like 进行错误选择的方式数。必须为非负数。 nsample：int或array_like 采样项目数。必须至少为1，且最多`ngood + nbad`。 size：int或tuple的整数，可选输出形状。如果给定形状是例如`（m， n， k）`，则 `m * n * k`默认值为None，在这种情况下返回单个值。
返回：	samples：ndarray或scalar 这些值都是[0，n]中的整数。

参数：

ngood：int或array_like

做出良好选择的方法数。必须为非负数。

nbad：int或array_like

进行错误选择的方式数。必须为非负数。

nsample：int或array_like

采样项目数。必须至少为1，且最多ngood + nbad。

size：int或tuple的整数，可选

输出形状。如果给定形状是例如（m， n， k），则 m * n * k默认值为None，在这种情况下返回单个值。

samples：ndarray或scalar

这些值都是[0，n]中的整数。

也可以看看

scipy.stats.distributions.hypergeom: 概率密度函数，分布或累积密度函数等。

笔记

超几何分布的概率密度为

其中 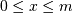$0 \le x \le m$ 和

对于P（x）x成功的概率，n = ngood，m = nbad，N =样本数。

考虑一个有黑色和白色大理石的缸，它们的颜色是黑色的，而nbad是白色的。如果你绘制没有替换的nsample球，那么超几何分布描述了绘制的样本中的黑球的分布。

注意，这种分布与二项分布非常相似，除了在这种情况下，绘制样本而不替换，而在二项式情况下，样本用替换来绘制（或者样本空间是无限的）。随着样本空间变大，该分布接近二项式。

参考文献

[R225]

Lentner，Marvin，“Elementary Applied Statistics”，Bogden和Quigley，1972。

[R226]

Weisstein，Eric W.“超几何分布”。来自MathWorld-Wolfram Web资源。http://mathworld.wolfram.com/HypergeometricDistribution.html

[R227]

维基百科，“超几何分布”，http://en.wikipedia.org/wiki/Hypergeometric_distribution

例子

从分布绘制样本：

>>> ngood, nbad, nsamp = 100, 2, 10
# number of good, number of bad, and number of samples
>>> s = np.random.hypergeometric(ngood, nbad, nsamp, 1000)
>>> hist(s)
#   note that it is very unlikely to grab both bad items

假设你有一个15白色和15黑色大理石的缸。如果你随机拉15个大理石，12个或更多的是一种颜色的可能性有多大？

>>> s = np.random.hypergeometric(15, 15, 15, 100000)
>>> sum(s>=12)/100000. + sum(s<=3)/100000.
#   answer = 0.003 ... pretty unlikely!