numpy.poly¶

numpy.poly(seq_of_zeros)[source]¶

找到具有给定的根序列的多项式的系数。

返回多项式的系数，其前导系数对于给定的零序列为一（多个根必须包括在序列中，次数与它们的多样性一样多；参见示例）。还可以给出方矩阵（或数组，其将被视为矩阵），在这种情况下返回矩阵的特征多项式的系数。

参数：	seq_of_zeros：array_like，shape（N，）或（N，N）多项式根序列，或正方形数组或矩阵对象。
返回：	c：ndarray 1D多项式系数从最高到最低的数组： `c[0] * x*(N) + c[1] x*(N-1) + ... + c[N-1] x + c[N]` where c[0] always equals 1.
上升：	ValueError 如果输入的形状错误（输入必须是1-D或正方形2-D数组）。

参数：

seq_of_zeros：array_like，shape（N，）或（N，N）

多项式根序列，或正方形数组或矩阵对象。

c：ndarray

1D多项式系数从最高到最低的数组：

c[0] * x**(N) + c[1] * x**(N-1) + ... + c[N-1] * x + c[N] where c[0] always equals 1.

上升：

ValueError

如果输入的形状错误（输入必须是1-D或正方形2-D数组）。

也可以看看

笔记

指定多项式的根仍然具有一个自由度，通常由未确定的超前系数表示。[R56]在此函数的情况下，该系数 - 返回的数组中的第一个 - 始终为1。（如果由于某种原因你有另外一点，目前利用该信息的唯一自动方法是使用polyfit。）

n -by- n矩阵A的特征多项式 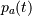$p_a(t)$ 由下式给出：

$p_a(t) = \mathrm{det}(t\, \mathbf{I} - \mathbf{A})$ ，

其中I是n -by- n单位矩阵。[R57]

参考文献

[R56]

(1, 2) M. Sullivan and M. Sullivan, III, “Algebra and Trignometry, Enhanced With Graphing Utilities,” Prentice-Hall, pg. 318，1996。

[R57]

（1，2） G.Strang，“Linear Algebra and Its Applications，第2版，”Academic Press，182，1980。

例子

给定多项式的零的序列：

>>> np.poly((0, 0, 0)) # Multiple root example
array([1, 0, 0, 0])

上面的行代表z ** 3 + 0 * z ** 2 + 0 * z + 0。

>>> np.poly((-1./2, 0, 1./2))
array([ 1.  ,  0.  , -0.25,  0.  ])

上面的行代表z ** 3 - z / 4

>>> np.poly((np.random.random(1.)[0], 0, np.random.random(1.)[0]))
array([ 1.        , -0.77086955,  0.08618131,  0.        ]) #random

给定一个正方形数组对象：

>>> P = np.array([[0, 1./3], [-1./2, 0]])
>>> np.poly(P)
array([ 1.        ,  0.        ,  0.16666667])

或方矩阵对象：

>>> np.poly(np.matrix(P))
array([ 1.        ,  0.        ,  0.16666667])

注意在所有情况下，领先的系数总是1。