去噪自动编码器（dA）

注意

本节假设读者已经阅读过使用逻辑回归分析MNIST数字和多层感知器。此外，它使用以下Theano函数和概念：T.tanh、共享变量、基本算术操作、T.grad、随机数，floatX。如果你打算在GPU上运行代码还需阅读GPU。

注意

此部分的代码可从此处下载。

去噪自动编码器（dA）是经典自动编码器的扩展，它在[Vincent08]中引入，用于深层网络的构建块。我们将以自动编码器的简短讨论开始教程。

自动编码器

有关自动编码器的概述，请参见[Bengio09]的第4.6节。自动编码器接受输入并且通过确定性映射首先将其（利用编码器）映射到一个隐藏表示，即：

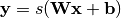
其中是非线性的，例如sigmoid。然后将潜在表示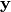或编码映射回（使用解码器）一个重构，它具有与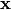相同的形状。映射通过类似的变换发生，例如：

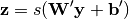
（这里，上标符号不表示矩阵转置。）应被视为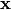的预测，给定编码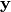。可选地，反向映射的权重矩阵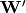可以被约束为正向映射的转置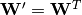：。这被称为绑定权重。优化该模型的参数（即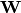、、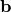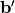，如果不使用绑定权重还有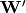），使得平均重构误差最小化。

重构误差可以以许多方式测量，这取决于给定编码时对输入分布的适当假设。可以使用传统的平方误差 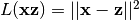。如果输入被解释为位向量或位概率的向量，则可以使用重构的交叉熵：

有个希望是编码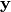是一个分布式表示，它捕获数据中主要变化因子的坐标。这类似于主成分上的投影将捕获数据中的主要变化因子的方式。实际上，如果存在一个线性隐藏层（编码）并且使用均方误差准则来训练网络，则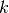个隐藏单元学习投影输入的开始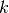个数据的主成分。如果隐藏层是非线性的，自动编码器的行为不同于PCA，具有捕获输入分布的多模态方面的能力。当构建深度自动编码器[Hinton06]时，考虑堆叠多个编码器（及其相应的解码器）时，不用PCA变得更加重要。

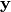因为被视为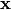的有损压缩，所以对于所有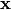，它不能是一个好的（小损耗）压缩。优化使其成为训练样本的良好压缩，并且希望用于其它输入，而不是用于任意输入。这是自动编码器概括的意义：它从与训练样本相同的分布给出测试样本上的低重构误差，但是通常在从输入空间随机选择的采样上具有高重构误差。

我们希望使用Theano以类的形式实现一个自动编码器，它可以在以后用于构造一个堆叠自动编码器。第一步是为自动编码器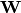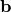，和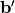的参数创建共享变量。（由于我们在本教程中使用绑定权重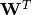，将用于）：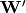

    def __init__(
        self,
        numpy_rng,
        theano_rng=None,
        input=None,
        n_visible=784,
        n_hidden=500,
        W=None,
        bhid=None,
        bvis=None
    ):
        """
        Initialize the dA class by specifying the number of visible units (the
        dimension d of the input ), the number of hidden units ( the dimension
        d' of the latent or hidden space ) and the corruption level. The
        constructor also receives symbolic variables for the input, weights and
        bias. Such a symbolic variables are useful when, for example the input
        is the result of some computations, or when weights are shared between
        the dA and an MLP layer. When dealing with SdAs this always happens,
        the dA on layer 2 gets as input the output of the dA on layer 1,
        and the weights of the dA are used in the second stage of training
        to construct an MLP.

        :type numpy_rng: numpy.random.RandomState
        :param numpy_rng: number random generator used to generate weights

        :type theano_rng: theano.tensor.shared_randomstreams.RandomStreams
        :param theano_rng: Theano random generator; if None is given one is
                     generated based on a seed drawn from `rng`

        :type input: theano.tensor.TensorType
        :param input: a symbolic description of the input or None for
                      standalone dA

        :type n_visible: int
        :param n_visible: number of visible units

        :type n_hidden: int
        :param n_hidden:  number of hidden units

        :type W: theano.tensor.TensorType
        :param W: Theano variable pointing to a set of weights that should be
                  shared belong the dA and another architecture; if dA should
                  be standalone set this to None

        :type bhid: theano.tensor.TensorType
        :param bhid: Theano variable pointing to a set of biases values (for
                     hidden units) that should be shared belong dA and another
                     architecture; if dA should be standalone set this to None

        :type bvis: theano.tensor.TensorType
        :param bvis: Theano variable pointing to a set of biases values (for
                     visible units) that should be shared belong dA and another
                     architecture; if dA should be standalone set this to None


        """
        self.n_visible = n_visible
        self.n_hidden = n_hidden

        # create a Theano random generator that gives symbolic random values
        if not theano_rng:
            theano_rng = RandomStreams(numpy_rng.randint(2 ** 30))

        # note : W' was written as `W_prime` and b' as `b_prime`
        if not W:
            # W is initialized with `initial_W` which is uniformely sampled
            # from -4*sqrt(6./(n_visible+n_hidden)) and
            # 4*sqrt(6./(n_hidden+n_visible))the output of uniform if
            # converted using asarray to dtype
            # theano.config.floatX so that the code is runable on GPU
            initial_W = numpy.asarray(
                numpy_rng.uniform(
                    low=-4 * numpy.sqrt(6. / (n_hidden + n_visible)),
                    high=4 * numpy.sqrt(6. / (n_hidden + n_visible)),
                    size=(n_visible, n_hidden)
                ),
                dtype=theano.config.floatX
            )
            W = theano.shared(value=initial_W, name='W', borrow=True)

        if not bvis:
            bvis = theano.shared(
                value=numpy.zeros(
                    n_visible,
                    dtype=theano.config.floatX
                ),
                borrow=True
            )

        if not bhid:
            bhid = theano.shared(
                value=numpy.zeros(
                    n_hidden,
                    dtype=theano.config.floatX
                ),
                name='b',
                borrow=True
            )

        self.W = W
        # b corresponds to the bias of the hidden
        self.b = bhid
        # b_prime corresponds to the bias of the visible
        self.b_prime = bvis
        # tied weights, therefore W_prime is W transpose
        self.W_prime = self.W.T
        self.theano_rng = theano_rng
        # if no input is given, generate a variable representing the input
        if input is None:
            # we use a matrix because we expect a minibatch of several
            # examples, each example being a row
            self.x = T.dmatrix(name='input')
        else:
            self.x = input

        self.params = [self.W, self.b, self.b_prime]

注意，我们将符号input作为参数传递给自动编码器。这是为了我们可以连接自动编码器的层以形成深网络：层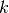的符号输出（上面的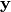）将是层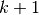的符号输入。

现在我们可以将潜在表示和重构信号的计算表示为：

    def get_hidden_values(self, input):
        """ Computes the values of the hidden layer """
        return T.nnet.sigmoid(T.dot(input, self.W) + self.b)

    def get_reconstructed_input(self, hidden):
        """Computes the reconstructed input given the values of the
        hidden layer

        """
        return T.nnet.sigmoid(T.dot(hidden, self.W_prime) + self.b_prime)

使用这些函数，我们可以如下计算随机梯度下降一个步骤的cost和updates：

    def get_cost_updates(self, corruption_level, learning_rate):
        """ This function computes the cost and the updates for one trainng
        step of the dA """

        tilde_x = self.get_corrupted_input(self.x, corruption_level)
        y = self.get_hidden_values(tilde_x)
        z = self.get_reconstructed_input(y)
        # note : we sum over the size of a datapoint; if we are using
        #        minibatches, L will be a vector, with one entry per
        #        example in minibatch
        L = - T.sum(self.x * T.log(z) + (1 - self.x) * T.log(1 - z), axis=1)
        # note : L is now a vector, where each element is the
        #        cross-entropy cost of the reconstruction of the
        #        corresponding example of the minibatch. We need to
        #        compute the average of all these to get the cost of
        #        the minibatch
        cost = T.mean(L)

        # compute the gradients of the cost of the `dA` with respect
        # to its parameters
        gparams = T.grad(cost, self.params)
        # generate the list of updates
        updates = [
            (param, param - learning_rate * gparam)
            for param, gparam in zip(self.params, gparams)
        ]

        return (cost, updates)

现在可以定义一个函数，对它进行迭代应用将更新参数W、b和b_prime，使得重构cost近似最小化。

    da = dA(
        numpy_rng=rng,
        theano_rng=theano_rng,
        input=x,
        n_visible=28 * 28,
        n_hidden=500
    )

    cost, updates = da.get_cost_updates(
        corruption_level=0.,
        learning_rate=learning_rate
    )

    train_da = theano.function(
        [index],
        cost,
        updates=updates,
        givens={
            x: train_set_x[index * batch_size: (index + 1) * batch_size]
        }
    )

    start_time = timeit.default_timer()

    ############
    # TRAINING #
    ############

    # go through training epochs
    for epoch in range(training_epochs):
        # go through trainng set
        c = []
        for batch_index in range(n_train_batches):
            c.append(train_da(batch_index))

        print('Training epoch %d, cost ' % epoch, numpy.mean(c, dtype='float64'))

    end_time = timeit.default_timer()

    training_time = (end_time - start_time)

    print(('The no corruption code for file ' +
           os.path.split(__file__)[1] +
           ' ran for %.2fm' % ((training_time) / 60.)), file=sys.stderr)
    image = Image.fromarray(
        tile_raster_images(X=da.W.get_value(borrow=True).T,
                           img_shape=(28, 28), tile_shape=(10, 10),
                           tile_spacing=(1, 1)))
    image.save('filters_corruption_0.png')

    # start-snippet-3
    #####################################
    # BUILDING THE MODEL CORRUPTION 30% #
    #####################################

    rng = numpy.random.RandomState(123)
    theano_rng = RandomStreams(rng.randint(2 ** 30))

    da = dA(
        numpy_rng=rng,
        theano_rng=theano_rng,
        input=x,
        n_visible=28 * 28,
        n_hidden=500
    )

    cost, updates = da.get_cost_updates(
        corruption_level=0.3,
        learning_rate=learning_rate
    )

    train_da = theano.function(
        [index],
        cost,
        updates=updates,
        givens={
            x: train_set_x[index * batch_size: (index + 1) * batch_size]
        }
    )

    start_time = timeit.default_timer()

    ############
    # TRAINING #
    ############

    # go through training epochs
    for epoch in range(training_epochs):
        # go through trainng set
        c = []
        for batch_index in range(n_train_batches):
            c.append(train_da(batch_index))

        print('Training epoch %d, cost ' % epoch, numpy.mean(c, dtype='float64'))

    end_time = timeit.default_timer()

    training_time = (end_time - start_time)

    print(('The 30% corruption code for file ' +
           os.path.split(__file__)[1] +
           ' ran for %.2fm' % (training_time / 60.)), file=sys.stderr)
    # end-snippet-3

    # start-snippet-4
    image = Image.fromarray(tile_raster_images(
        X=da.W.get_value(borrow=True).T,
        img_shape=(28, 28), tile_shape=(10, 10),
        tile_spacing=(1, 1)))
    image.save('filters_corruption_30.png')
    # end-snippet-4

    os.chdir('../')


if __name__ == '__main__':
    test_dA()

如果除了最小化重建误差之外没有约束，可以期望具有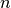个输入和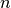（或更大）个维度编码的自动编码器来学习身份函数，仅将输入映射到其拷贝。这样的自动编码器不会将测试样本（依据训练的分布）与其他输入配置区分开。

令人惊讶的是，在[Bengio07]中报道的实验表明，在实践中，当使用随机梯度下降训练时，具有比输入更多隐藏单元（称为过完备）的非线性自动编码器产生有用的表示。（这里，“有用”意味着将编码作为输入的网络具有低分类误差）。

简单的解释是带有提前停止的随机梯度下降类似于参数的L2正则化。为了实现连续输入的完美重构，具有非线性隐藏单元的单隐层自动编码器（正如在上面的代码中）在第一（编码）层中需要非常小的权重，以使得非线性隐藏单元到它们的线性区域中，并且在第二（解码）层中具有非常大的权重。使用二元输入，还需要非常大的权重来完全最小化重建误差。因为隐式或显式正则化使得难以达到大权重解决方案，所以优化算法找到的编码只对类似于训练集中的样本工作得很好，这就是我们想要的。这意味着表示正在利用训练集中存在的统计规律，而不是仅仅学习复制输入。

还存在其他方法，通过该方法可以防止具有比输入更多的隐藏单元的自动编码器学习身份功能，在其隐藏表示中捕获对输入有用的东西。一个是添加稀疏（强制许多隐藏单位为零或接近零）。稀疏性已经被许多[Ranzato07] [Lee08]文献非常成功地利用。另一个是在从输入到重建的变换中添加随机性。该技术用于受限玻尔兹曼机（稍后在Restricted Boltzmann Machines (RBM)中讨论）以及下面讨论的去噪自动编码器中。

去噪自动编码器

去噪自动编码器背后的想法很简单。为了迫使隐藏层发现更鲁棒的特征并且防止它简单地学习身份，我们训练自动编码器以从它的损坏版本重建输入。

去噪自动编码器是自动编码器的随机版本。直观地，去噪自动编码器做两件事：尝试对输入进行编码（保留关于输入的信息），并且尝试撤消随机应用于自动编码器的输入的损坏过程的影响。后者只能通过捕获输入之间的统计依赖性来完成。可以从不同的角度（流形学习观点，随机运算符观点，自下而上信息理论观点，自上而下 - 生成模型观点）理解去噪自动编码器，所有这些解释在[Vincent08] 。有关自动编码器的概述，另见[Bengio09]的第7.2节。

在[Vincent08]中，随机破坏过程随机设置一些输入为0（多达一半）。因此，对于随机选择的丢失模式的子集，去噪自动编码器试图从未被破坏（即非丢失）的值预测被破坏（即丢失）的值。注意如何能够从剩余的变量中预测任何子集的变量是完全捕获一组变量之间的联合分布的充分条件（这是Gibbs采样的工作原理）。

要将autoencoder类转换为去噪自动编码器类，我们所需要做的就是添加一个对输入进行操作的随机损坏步骤。输入可以在许多方面损坏，但在本教程中，我们将坚持使输入为零的随机掩码输入的原始损坏机制。下面的代码只是这样：

    def get_corrupted_input(self, input, corruption_level):
        """This function keeps ``1-corruption_level`` entries of the inputs the
        same and zero-out randomly selected subset of size ``coruption_level``
        Note : first argument of theano.rng.binomial is the shape(size) of
               random numbers that it should produce
               second argument is the number of trials
               third argument is the probability of success of any trial

                this will produce an array of 0s and 1s where 1 has a
                probability of 1 - ``corruption_level`` and 0 with
                ``corruption_level``

                The binomial function return int64 data type by
                default.  int64 multiplicated by the input
                type(floatX) always return float64.  To keep all data
                in floatX when floatX is float32, we set the dtype of
                the binomial to floatX. As in our case the value of
                the binomial is always 0 or 1, this don't change the
                result. This is needed to allow the gpu to work
                correctly as it only support float32 for now.

        """
        return self.theano_rng.binomial(size=input.shape, n=1,
                                        p=1 - corruption_level,
                                        dtype=theano.config.floatX) * input

在堆叠自动编码器类（堆叠自动编码器）中，dA类的权重必须与对应的Sigmoid层的权重共享。因此，dA的构造函数也会获得指向共享参数的Theano变量。如果这些参数保留为None，那么将构造新的参数。

最终去噪自动编码器类变为：

class dA(object):
    """Denoising Auto-Encoder class (dA)

    A denoising autoencoders tries to reconstruct the input from a corrupted
    version of it by projecting it first in a latent space and reprojecting
    it afterwards back in the input space. Please refer to Vincent et al.,2008
    for more details. If x is the input then equation (1) computes a partially
    destroyed version of x by means of a stochastic mapping q_D. Equation (2)
    computes the projection of the input into the latent space. Equation (3)
    computes the reconstruction of the input, while equation (4) computes the
    reconstruction error.

    .. math::

        \tilde{x} ~ q_D(\tilde{x}|x)                                     (1)

        y = s(W \tilde{x} + b)                                           (2)

        x = s(W' y  + b')                                                (3)

        L(x,z) = -sum_{k=1}^d [x_k \log z_k + (1-x_k) \log( 1-z_k)]      (4)

    """

    def __init__(
        self,
        numpy_rng,
        theano_rng=None,
        input=None,
        n_visible=784,
        n_hidden=500,
        W=None,
        bhid=None,
        bvis=None
    ):
        """
        Initialize the dA class by specifying the number of visible units (the
        dimension d of the input ), the number of hidden units ( the dimension
        d' of the latent or hidden space ) and the corruption level. The
        constructor also receives symbolic variables for the input, weights and
        bias. Such a symbolic variables are useful when, for example the input
        is the result of some computations, or when weights are shared between
        the dA and an MLP layer. When dealing with SdAs this always happens,
        the dA on layer 2 gets as input the output of the dA on layer 1,
        and the weights of the dA are used in the second stage of training
        to construct an MLP.

        :type numpy_rng: numpy.random.RandomState
        :param numpy_rng: number random generator used to generate weights

        :type theano_rng: theano.tensor.shared_randomstreams.RandomStreams
        :param theano_rng: Theano random generator; if None is given one is
                     generated based on a seed drawn from `rng`

        :type input: theano.tensor.TensorType
        :param input: a symbolic description of the input or None for
                      standalone dA

        :type n_visible: int
        :param n_visible: number of visible units

        :type n_hidden: int
        :param n_hidden:  number of hidden units

        :type W: theano.tensor.TensorType
        :param W: Theano variable pointing to a set of weights that should be
                  shared belong the dA and another architecture; if dA should
                  be standalone set this to None

        :type bhid: theano.tensor.TensorType
        :param bhid: Theano variable pointing to a set of biases values (for
                     hidden units) that should be shared belong dA and another
                     architecture; if dA should be standalone set this to None

        :type bvis: theano.tensor.TensorType
        :param bvis: Theano variable pointing to a set of biases values (for
                     visible units) that should be shared belong dA and another
                     architecture; if dA should be standalone set this to None


        """
        self.n_visible = n_visible
        self.n_hidden = n_hidden

        # create a Theano random generator that gives symbolic random values
        if not theano_rng:
            theano_rng = RandomStreams(numpy_rng.randint(2 ** 30))

        # note : W' was written as `W_prime` and b' as `b_prime`
        if not W:
            # W is initialized with `initial_W` which is uniformely sampled
            # from -4*sqrt(6./(n_visible+n_hidden)) and
            # 4*sqrt(6./(n_hidden+n_visible))the output of uniform if
            # converted using asarray to dtype
            # theano.config.floatX so that the code is runable on GPU
            initial_W = numpy.asarray(
                numpy_rng.uniform(
                    low=-4 * numpy.sqrt(6. / (n_hidden + n_visible)),
                    high=4 * numpy.sqrt(6. / (n_hidden + n_visible)),
                    size=(n_visible, n_hidden)
                ),
                dtype=theano.config.floatX
            )
            W = theano.shared(value=initial_W, name='W', borrow=True)

        if not bvis:
            bvis = theano.shared(
                value=numpy.zeros(
                    n_visible,
                    dtype=theano.config.floatX
                ),
                borrow=True
            )

        if not bhid:
            bhid = theano.shared(
                value=numpy.zeros(
                    n_hidden,
                    dtype=theano.config.floatX
                ),
                name='b',
                borrow=True
            )

        self.W = W
        # b corresponds to the bias of the hidden
        self.b = bhid
        # b_prime corresponds to the bias of the visible
        self.b_prime = bvis
        # tied weights, therefore W_prime is W transpose
        self.W_prime = self.W.T
        self.theano_rng = theano_rng
        # if no input is given, generate a variable representing the input
        if input is None:
            # we use a matrix because we expect a minibatch of several
            # examples, each example being a row
            self.x = T.dmatrix(name='input')
        else:
            self.x = input

        self.params = [self.W, self.b, self.b_prime]

    def get_corrupted_input(self, input, corruption_level):
        """This function keeps ``1-corruption_level`` entries of the inputs the
        same and zero-out randomly selected subset of size ``coruption_level``
        Note : first argument of theano.rng.binomial is the shape(size) of
               random numbers that it should produce
               second argument is the number of trials
               third argument is the probability of success of any trial

                this will produce an array of 0s and 1s where 1 has a
                probability of 1 - ``corruption_level`` and 0 with
                ``corruption_level``

                The binomial function return int64 data type by
                default.  int64 multiplicated by the input
                type(floatX) always return float64.  To keep all data
                in floatX when floatX is float32, we set the dtype of
                the binomial to floatX. As in our case the value of
                the binomial is always 0 or 1, this don't change the
                result. This is needed to allow the gpu to work
                correctly as it only support float32 for now.

        """
        return self.theano_rng.binomial(size=input.shape, n=1,
                                        p=1 - corruption_level,
                                        dtype=theano.config.floatX) * input

    def get_hidden_values(self, input):
        """ Computes the values of the hidden layer """
        return T.nnet.sigmoid(T.dot(input, self.W) + self.b)

    def get_reconstructed_input(self, hidden):
        """Computes the reconstructed input given the values of the
        hidden layer

        """
        return T.nnet.sigmoid(T.dot(hidden, self.W_prime) + self.b_prime)

    def get_cost_updates(self, corruption_level, learning_rate):
        """ This function computes the cost and the updates for one trainng
        step of the dA """

        tilde_x = self.get_corrupted_input(self.x, corruption_level)
        y = self.get_hidden_values(tilde_x)
        z = self.get_reconstructed_input(y)
        # note : we sum over the size of a datapoint; if we are using
        #        minibatches, L will be a vector, with one entry per
        #        example in minibatch
        L = - T.sum(self.x * T.log(z) + (1 - self.x) * T.log(1 - z), axis=1)
        # note : L is now a vector, where each element is the
        #        cross-entropy cost of the reconstruction of the
        #        corresponding example of the minibatch. We need to
        #        compute the average of all these to get the cost of
        #        the minibatch
        cost = T.mean(L)

        # compute the gradients of the cost of the `dA` with respect
        # to its parameters
        gparams = T.grad(cost, self.params)
        # generate the list of updates
        updates = [
            (param, param - learning_rate * gparam)
            for param, gparam in zip(self.params, gparams)
        ]

        return (cost, updates)

合在一起

现在很容易构造一个我们的dA类的实例并训练它。

    # allocate symbolic variables for the data
    index = T.lscalar()    # index to a [mini]batch
    x = T.matrix('x')  # the data is presented as rasterized images

    #####################################
    # BUILDING THE MODEL CORRUPTION 30% #
    #####################################

    rng = numpy.random.RandomState(123)
    theano_rng = RandomStreams(rng.randint(2 ** 30))

    da = dA(
        numpy_rng=rng,
        theano_rng=theano_rng,
        input=x,
        n_visible=28 * 28,
        n_hidden=500
    )

    cost, updates = da.get_cost_updates(
        corruption_level=0.3,
        learning_rate=learning_rate
    )

    train_da = theano.function(
        [index],
        cost,
        updates=updates,
        givens={
            x: train_set_x[index * batch_size: (index + 1) * batch_size]
        }
    )

    start_time = timeit.default_timer()

    ############
    # TRAINING #
    ############

    # go through training epochs
    for epoch in range(training_epochs):
        # go through trainng set
        c = []
        for batch_index in range(n_train_batches):
            c.append(train_da(batch_index))

        print('Training epoch %d, cost ' % epoch, numpy.mean(c, dtype='float64'))

    end_time = timeit.default_timer()

    training_time = (end_time - start_time)

    print(('The 30% corruption code for file ' +
           os.path.split(__file__)[1] +
           ' ran for %.2fm' % (training_time / 60.)), file=sys.stderr)

为了感知学习到的网络，我们将绘制出filter（由权重矩阵定义）。但是，请记住，这不提供整个故事，因为我们忽略偏差，并将权重绘制成乘法常数（权重转换为0和1之间的值）。

要绘制我们的filter，我们需要tile_raster_images（参见绘制样本和filter）的帮助，所以我们鼓励读者学习它。还使用Python图像库的帮助，以下代码行将filter保存为图像：

    image = Image.fromarray(tile_raster_images(
        X=da.W.get_value(borrow=True).T,
        img_shape=(28, 28), tile_shape=(10, 10),
        tile_spacing=(1, 1)))
    image.save('filters_corruption_30.png')

运行代码

运行代码：

python dA.py

当我们不使用任何噪声时，产生的filter是：

30％噪声的filter：