numpy.random.random_integers¶

numpy.random.random_integers(low, high=None, size=None)¶

低和高之间的np.int类型的随机整数（含）。

从闭合区间[低，高]中的“离散均匀”分布返回np.int类型的随机整数。如果高为无（默认值），则结果来自[1，低]。np.int类型转换为Python 2用于“短”整数的C long类型，其精度是平台相关的。

此函数已被弃用。请改用randint。

自1.11.0版起已弃用。

参数：	低：int 从分布中绘制的最低（有符号）整数（除非`high=None`，在此情况下此参数是最高这样的整数）。高：int，可选如果提供，从分布中绘制的最大（有符号）整数（如果`high=None`，请参见上面的行为）。 size：int或tuple的整数，可选输出形状。如果给定形状是例如`（m， n， k）`，则 `m * n * k`默认值为None，在这种情况下返回单个值。
返回：	out：int或ndarray的整数 size从合适的分布中随机整数的数组，或者如果size未提供，则单个这样的随机int。

参数：

低：int

从分布中绘制的最低（有符号）整数（除非high=None，在此情况下此参数是最高这样的整数）。

高：int，可选

如果提供，从分布中绘制的最大（有符号）整数（如果high=None，请参见上面的行为）。

size：int或tuple的整数，可选

输出形状。如果给定形状是例如（m， n， k），则 m * n * k默认值为None，在这种情况下返回单个值。

out：int或ndarray的整数

size从合适的分布中随机整数的数组，或者如果size未提供，则单个这样的随机int。

也可以看看

random.randint: Similar to random_integers, only for the half-open interval [low, high), and 0 is the lowest value if high is omitted.

笔记

要从a和b之间的N个均匀间隔的浮点数进行采样，请使用：

a + (b - a) * (np.random.random_integers(N) - 1) / (N - 1.)

例子

>>> np.random.random_integers(5)
4
>>> type(np.random.random_integers(5))
<type 'int'>
>>> np.random.random_integers(5, size=(3.,2.))
array([[5, 4],
       [3, 3],
       [4, 5]])

从0到2.5之间的五个均匀间隔数字（，即，从集合 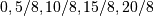${0, 5/8, 10/8, 15/8, 20/8}$ ）中选择五个随机数字：

>>> 2.5 * (np.random.random_integers(5, size=(5,)) - 1) / 4.
array([ 0.625,  1.25 ,  0.625,  0.625,  2.5  ])

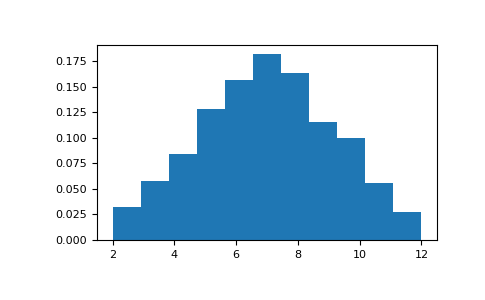
辊两面六面骰子1000次，总结结果：

>>> d1 = np.random.random_integers(1, 6, 1000)
>>> d2 = np.random.random_integers(1, 6, 1000)
>>> dsums = d1 + d2

以直方图显示结果：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(dsums, 11, normed=True)
>>> plt.show()

（源代码，png，pdf）

../../_images/numpy-random-random_integers-1.png