numpy.linalg.eig¶

numpy.linalg.eig(a)[source]¶

计算正方形数组的特征值和右特征向量。

参数：	a：（...，M，M）数组将计算特征值和右特征向量的矩阵
返回：	w：（...，M）数组特征值，每个根据其多重性重复。特征值不必是有序的。结果数组将是复杂类型，除非虚部为零，在这种情况下，它将被转换为实数类型。当a是实数时，得到的特征值将是实数（0虚数部分）或出现在共轭对 v：（...，M，M）数组归一化（单位“长度”）特征向量，使得列`v[:,i]`是对应于特征值`w[i]`
引发：	LinAlgError 如果特征值计算不收敛。

参数：

a：（...，M，M）数组

将计算特征值和右特征向量的矩阵

w：（...，M）数组

特征值，每个根据其多重性重复。特征值不必是有序的。结果数组将是复杂类型，除非虚部为零，在这种情况下，它将被转换为实数类型。当a是实数时，得到的特征值将是实数（0虚数部分）或出现在共轭对

v：（...，M，M）数组

归一化（单位“长度”）特征向量，使得列v[:,i]是对应于特征值w[i]

引发：

LinAlgError

如果特征值计算不收敛。

另见

eigvals: 非对称数组的特征值。
eigh: 对称或Hermitian（共轭对称）数组的特征值和特征向量。
eigvalsh: 对称或Hermitian（共轭对称）数组的特征值。

注

版本1.8.0中的新功能。

广播规则适用，有关详细信息，请参阅numpy.linalg文档。

这是使用_geev LAPACK例程来实现的，其计算一般方阵数组的特征值和特征向量。

The number w is an eigenvalue of a if there exists a vector v such that dot(a,v) = w * v. Thus, the arrays a, w, and v satisfy the equations dot(a[:,:], v[:,i]) = w[i] * v[:,i] for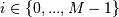 $i \in \{0,...,M-1\}$ .

特征向量的数组v可能不是最大秩，即，一些列可以是线性相关的，尽管舍入误差可能模糊该事实。如果特征值全部不同，则理论上特征向量是线性无关的。Likewise, the (complex-valued) matrix of eigenvectors v is unitary if the matrix a is normal, i.e., if dot(a, a.H) = dot(a.H, a), where a.H denotes the conjugate transpose of a.

最后，要强调的是，v由a的右侧（如右侧）特征向量组成。A vector y satisfying dot(y.T, a) = z * y.T for some number z is called a left eigenvector of a, and, in general, the left and right eigenvectors of a matrix are not necessarily the (perhaps conjugate) transposes of each other.

参考文献

G.Strang，Linear Algebra and Its Applications，第2版，Orlando，FL，Academic Press，Inc.，1980，

例子

>>> from numpy import linalg as LA

（几乎）平凡的例子与真实e值和e向量。

>>> w, v = LA.eig(np.diag((1, 2, 3)))
>>> w; v
array([ 1.,  2.,  3.])
array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

具有复杂e值和e向量的真实矩阵；注意e值是彼此的复共轭。

>>> w, v = LA.eig(np.array([[1, -1], [1, 1]]))
>>> w; v
array([ 1. + 1.j,  1. - 1.j])
array([[ 0.70710678+0.j        ,  0.70710678+0.j        ],
       [ 0.00000000-0.70710678j,  0.00000000+0.70710678j]])

具有真实e值（但复值e向量）的复值矩阵；注意a.conj()。T = a，即a是Hermitian。

>>> a = np.array([[1, 1j], [-1j, 1]])
>>> w, v = LA.eig(a)
>>> w; v
array([  2.00000000e+00+0.j,   5.98651912e-36+0.j]) # i.e., {2, 0}
array([[ 0.00000000+0.70710678j,  0.70710678+0.j        ],
       [ 0.70710678+0.j        ,  0.00000000+0.70710678j]])

小心舍入错误！

>>> a = np.array([[1 + 1e-9, 0], [0, 1 - 1e-9]])
>>> # Theor. e-values are 1 +/- 1e-9
>>> w, v = LA.eig(a)
>>> w; v
array([ 1.,  1.])
array([[ 1.,  0.],
       [ 0.,  1.]])