numpy.kaiser

numpy.kaiser(M, beta)

返回Kaiser窗口。

凯塞窗是使用贝塞尔函数形成的锥形。

参数：

M：int

输出窗口中的点数。如果为零或更小，则返回一个空数组。

beta：float

窗口形状参数。

返回：

out：数组

窗口，最大值归一化为1（仅当样本数为奇数时才显示该值）。

也可以看看

bartlett，blackman，hamming，hanning

笔记

Kaiser窗口定义为

与

其中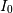是修改的零阶贝塞尔函数。

Kaiser被命名为Jim Kaiser，他发现了基于Bessel函数的DPSS窗口的简单近似。Kaiser窗口是数字生成球形序列或Slepian窗口的非常好的近似，其是使窗口的主瓣相对于总能量的能量最大化的变换。

Kaiser可以通过改变beta参数来近似许多其他窗口。

beta	窗口的形状
0	长方形
5	类似汉明
6	类似于汉宁
8.6	类似于布莱克曼

beta值为14可能是一个很好的起点。注意，当β变大时，窗口变窄，因此样本的数量需要足够大以采样越来越窄的尖峰，否则NaN将被返回。

大多数对Kaiser窗口的引用来自信号处理文献，其中它被用作用于平滑值的许多窗口函数中的一个。它也称为变迹（意指“去除脚”，即在采样信号的开始和结束处的平滑不连续性）或渐变函数。

参考文献

[R34]

J.D.Kaiser，“Digital Filters”-Ch7 in“Systems analysis by digital computer”，Editors：F.F.Kuo和J.F.Kaiser，第218-285页。John Wiley and Sons，New York，（1966）。

[R35]

E.R.Kanasewich，“Time Sequence Analysis in Geophysics”，The University of Alberta Press，1975，pp。177-178。

[R36]

维基百科，“窗口函数”，http://en.wikipedia.org/wiki/Window_function

例子

>>> np.kaiser(12, 14)
array([  7.72686684e-06,   3.46009194e-03,   4.65200189e-02,
         2.29737120e-01,   5.99885316e-01,   9.45674898e-01,
         9.45674898e-01,   5.99885316e-01,   2.29737120e-01,
         4.65200189e-02,   3.46009194e-03,   7.72686684e-06])

绘制窗口和频率响应：

>>> from numpy.fft import fft, fftshift
>>> window = np.kaiser(51, 14)
>>> plt.plot(window)
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.title("Kaiser window")
<matplotlib.text.Text object at 0x...>
>>> plt.ylabel("Amplitude")
<matplotlib.text.Text object at 0x...>
>>> plt.xlabel("Sample")
<matplotlib.text.Text object at 0x...>
>>> plt.show()

>>> plt.figure()
<matplotlib.figure.Figure object at 0x...>
>>> A = fft(window, 2048) / 25.5
>>> mag = np.abs(fftshift(A))
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(mag)
>>> response = np.clip(response, -100, 100)
>>> plt.plot(freq, response)
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.title("Frequency response of Kaiser window")
<matplotlib.text.Text object at 0x...>
>>> plt.ylabel("Magnitude [dB]")
<matplotlib.text.Text object at 0x...>
>>> plt.xlabel("Normalized frequency [cycles per sample]")
<matplotlib.text.Text object at 0x...>
>>> plt.axis('tight')
(-0.5, 0.5, -100.0, ...)
>>> plt.show()