numpy.cov¶
-
numpy.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)[source]¶ 估计协方差矩阵,给定数据和权重。
协方差表示两个变量一起变化的水平。If we examine N-dimensional samples,
![X = [x_1, x_2, ... x_N]^T](../../_images/math/8d14fb48024fc0aaeed58a8b7e012bf142402c41.png) , then the covariance matrix element
, then the covariance matrix element 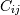 is the covariance of
is the covariance of 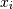 and
and 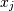 . 元素
. 元素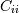 是
是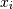 的方差。
的方差。有关算法的概述,请参见注释。
参数: m:array_like
包含多个变量和观察值的1-D或2-D数组。m的每一行代表一个变量,每一列都是对所有这些变量的单次观察。另请参阅下面的rowvar。
y:array_like,可选
另一组变量和观察值。y具有与m相同的形式。
rowvar:bool,可选
如果rowvar为True(默认值),则每行代表一个变量,在列中有观察值。否则,关系会转置:每个列表示一个变量,而行包含观察值。
bias:bool,可选
默认规范化(False)为
(N - 1),其中N是给出的观察的数量(无偏估计)。如果bias为True,则归一化为N。这些值可以通过在numpy versions> = 1.5中使用关键字ddof来覆盖。ddof:int,可选
如果
None,bias所隐含的默认值将被覆盖。Note thatddof=1will return the unbiased estimate, even if both fweights and aweights are specified, andddof=0will return the simple average. 有关详细信息,请参阅注释。默认值为None。版本1.5中的新功能。
fweights:array_like,int,可选
1-D数组整数频率权重;每个观察向量应当重复的次数。
版本1.10中的新功能。
aweights:array_like,可选
1-D数组的观测向量权重。这些相对权重对于被认为“重要”的观察来说通常较大,对于被认为较不“重要”的观察来说较小。如果
ddof=0,权重的数组可以用于向观察向量分配概率。版本1.10中的新功能。
返回: out:ndarray
变量的协方差矩阵。
也可以看看
corrcoef- 归一化协方差矩阵
笔记
Assume that the observations are in the columns of the observation array m and let
f = fweightsanda = aweightsfor brevity. 计算加权协方差的步骤如下:>>> w = f * a >>> v1 = np.sum(w) >>> v2 = np.sum(w * a) >>> m -= np.sum(m * w, axis=1, keepdims=True) / v1 >>> cov = np.dot(m * w, m.T) * v1 / (v1**2 - ddof * v2)
注意,当
a == 1时,归一化因子v1 / (v1 ** 2 - ddof * v2) / t11>转到1 / (np.sum(f) - t16 > ddof)。例子
考虑两个变量,
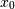 和
和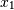 ,它们完全相关,但方向相反:
,它们完全相关,但方向相反:>>> x = np.array([[0, 2], [1, 1], [2, 0]]).T >>> x array([[0, 1, 2], [2, 1, 0]])
注意
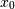 增加而
增加而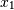 减少。协方差矩阵清楚地表明:
减少。协方差矩阵清楚地表明:>>> np.cov(x) array([[ 1., -1.], [-1., 1.]])
注意,示出
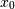 和
和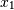 之间的相关性的元素
之间的相关性的元素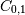 是负的。
是负的。此外,请注意x和y是如何组合的:
>>> x = [-2.1, -1, 4.3] >>> y = [3, 1.1, 0.12] >>> X = np.vstack((x,y)) >>> print(np.cov(X)) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print(np.cov(x, y)) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print(np.cov(x)) 11.71