numpy.histogram¶

numpy.histogram(a, bins=10, range=None, normed=False, weights=None, density=None)[source]¶

计算一组数据的直方图。

参数：	a：array_like 输入数据。在扁平数组上计算直方图。 bins：int或标量序列或str，可选如果bins是一个int，它定义了在给定范围（默认为10）中等宽单元格的数量。如果bin是序列，则它定义了块边缘，包括最右边缘，允许非均匀的块宽度。版本1.11.0中的新功能。如果bins是以下列表中的字符串，则`histogram`将使用所选方法来计算最佳bin宽度，因此计算bin数（参见t4>关于估计器的更多细节）从落入请求范围内的数据。尽管区间宽度对于该范围中的实际数据将是最佳的，但是将计算区间的数目以填充整个范围，包括空白部分。为了可视化，建议使用'auto'选项。不支持自动bin大小选择的加权数据。 '汽车' 最大的“sturges”和“fd”估计。提供良好的全方位性能 'fd'（Freedman Diaconis Estimator）鲁棒（弹性到异常值）估计器，考虑数据变异性和数据大小。 'doane' Sturges估计器的改进版本，与非正态数据集更好地工作。 'scott' 较不鲁棒的估计器，其考虑到数据变异性和数据大小。 '白饭' 估计器不考虑变化性，只考虑数据大小。通常高估需要的箱数。 'sturges' R的默认方法，只考虑数据大小。只对高斯数据最优，低估了大型非高斯数据集的二进制数。 'sqrt' 平方根（数据大小）估计器，由Excel和其他程序使用它的速度和简单性。范围：（float，float），可选仓的下限和上限。如果不提供，范围只是`（a.min()， a.max()）`。忽略范围之外的值。范围的第一个元素必须小于或等于第二个元素。范围也会影响自动bin计算。虽然基于范围内的实际数据计算bin宽度是最优的，但是bin计数将填充整个范围，包括不包含数据的部分。 normed：bool，可选此关键字在Numpy 1.6中已被弃用，原因是混乱/错误行为。它将在Numpy 2.0中删除。请改用`density`关键字。如果`False`，结果将包含每个bin中的样本数。如果`True`，则结果是在bin处的概率密度函数的值，被归一化，使得在该范围上的积分是1。注意，后一种行为被认为是具有不相等的bin宽度的bug；请改用`density`。权重：array_like，可选一个权重数组，形状与a相同。a中的每个值仅将其关联的权重贡献给bin计数（而不是1）。如果density为True，则权重被归一化，使得该范围上的密度的积分保持为1。密度：bool，可选如果`False`，结果将包含每个bin中的样本数。如果`True`，则结果是在bin处的概率密度函数的值，被归一化，使得在该范围上的积分是1。注意，直方图值的总和不会等于1，除非选择单位宽度的二进制位；它不是概率质量函数。覆盖`normed`关键字（如果给定）。
返回：	hist：数组直方图的值。有关可能的语义的描述，请参见密度和权重。 bin_edges：dtype float的数组返回bin边`(length(hist)+1)`。

参数：

a：array_like

输入数据。在扁平数组上计算直方图。

bins：int或标量序列或str，可选

如果bins是一个int，它定义了在给定范围（默认为10）中等宽单元格的数量。如果bin是序列，则它定义了块边缘，包括最右边缘，允许非均匀的块宽度。

版本1.11.0中的新功能。

如果bins是以下列表中的字符串，则histogram将使用所选方法来计算最佳bin宽度，因此计算bin数（参见t4>关于估计器的更多细节）从落入请求范围内的数据。尽管区间宽度对于该范围中的实际数据将是最佳的，但是将计算区间的数目以填充整个范围，包括空白部分。为了可视化，建议使用'auto'选项。不支持自动bin大小选择的加权数据。

'汽车'

最大的“sturges”和“fd”估计。提供良好的全方位性能

'fd'（Freedman Diaconis Estimator）

鲁棒（弹性到异常值）估计器，考虑数据变异性和数据大小。

'doane'

Sturges估计器的改进版本，与非正态数据集更好地工作。

'scott'

较不鲁棒的估计器，其考虑到数据变异性和数据大小。

'白饭'

估计器不考虑变化性，只考虑数据大小。通常高估需要的箱数。

'sturges'

R的默认方法，只考虑数据大小。只对高斯数据最优，低估了大型非高斯数据集的二进制数。

'sqrt'

平方根（数据大小）估计器，由Excel和其他程序使用它的速度和简单性。

范围：（float，float），可选

仓的下限和上限。如果不提供，范围只是（a.min()， a.max()）。忽略范围之外的值。范围的第一个元素必须小于或等于第二个元素。范围也会影响自动bin计算。虽然基于范围内的实际数据计算bin宽度是最优的，但是bin计数将填充整个范围，包括不包含数据的部分。

normed：bool，可选

此关键字在Numpy 1.6中已被弃用，原因是混乱/错误行为。它将在Numpy 2.0中删除。请改用density关键字。如果False，结果将包含每个bin中的样本数。如果True，则结果是在bin处的概率密度函数的值，被归一化，使得在该范围上的积分是1。注意，后一种行为被认为是具有不相等的bin宽度的bug；请改用density。

权重：array_like，可选

一个权重数组，形状与a相同。a中的每个值仅将其关联的权重贡献给bin计数（而不是1）。如果density为True，则权重被归一化，使得该范围上的密度的积分保持为1。

密度：bool，可选

如果False，结果将包含每个bin中的样本数。如果True，则结果是在bin处的概率密度函数的值，被归一化，使得在该范围上的积分是1。注意，直方图值的总和不会等于1，除非选择单位宽度的二进制位；它不是概率质量函数。

覆盖normed关键字（如果给定）。

hist：数组

直方图的值。有关可能的语义的描述，请参见密度和权重。

bin_edges：dtype float的数组

返回bin边(length(hist)+1)。

也可以看看

histogramdd，bincount，searchsorted，digitize

笔记

除了最后一个（最右边的）bin都是半开的。换句话说，如果bin是：

[1, 2, 3, 4]

那么第一个仓是[1， 2）（包括1，但不包括2），第二个， 3）。然而，最后一个仓是[3， 4]，其中包括 4。

版本1.11.0中的新功能。

估计箱的最佳数量的方法在文献中是充分的，并且受到直方图可视化的选择R的启发。注意，具有与 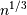$n^{1/3}$ 成比例的二进制数的数目是渐近最优的，这就是为什么其出现在大多数估计器中的原因。这些是简单的插入方法，为块数量提供良好的起点。在下面的等式中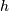， $h$ 是binwidth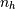， $n_h$ 是bin的个数。使用数据的ptp将计算bin数的所有估计值重新转换为bin宽度。最终bin计数从`` np.round（np.ceil（range / h））获得。

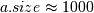'Auto'（'Sturges'和'FD'估计量的最大值）: 一个妥协，得到一个好的价值。对于小数据集，通常选择Sturges值，而较大的数据集通常默认为FD。避免了对于小数据集和大数据集的FD和Sturges的过分保守的行为。切换点通常 $a.size \approx 1000$ 。
'FD'（Freedman Diaconis Estimator）: binwidth与四分位距（IQR）成正比，与a.size的立方根成反比。对于小型数据集可能过于保守，但对大型数据集非常有用。IQR对异常值非常鲁棒。
'Scott': binwidth与数据的标准偏差成比例，并且与x.size的立方根成反比。对于小型数据集可能过于保守，但对大型数据集非常有用。标准偏差对异常值不是非常鲁棒。值在没有异常值的情况下与Freedman-Diaconis估计量非常相似。
'白饭': 二进制数的数量仅与a.size的立方根成正比。它倾向于高估仓的数量，并且不考虑数据变异性。
“Sturges”: 仓的数量是a.size的基础2对数。该估计量假定数据的正态性，并且对于较大的非正态数据集过于保守。这是R的hist方法中的默认方法。
'Doane': Sturges公式的改进版本，对非正态数据集产生更好的估计。该估计器尝试解释数据的偏斜。
'Sqrt': 最简单和最快的估计。只考虑数据大小。

例子

>>> np.histogram([1, 2, 1], bins=[0, 1, 2, 3])
(array([0, 2, 1]), array([0, 1, 2, 3]))
>>> np.histogram(np.arange(4), bins=np.arange(5), density=True)
(array([ 0.25,  0.25,  0.25,  0.25]), array([0, 1, 2, 3, 4]))
>>> np.histogram([[1, 2, 1], [1, 0, 1]], bins=[0,1,2,3])
(array([1, 4, 1]), array([0, 1, 2, 3]))

>>> a = np.arange(5)
>>> hist, bin_edges = np.histogram(a, density=True)
>>> hist
array([ 0.5,  0. ,  0.5,  0. ,  0. ,  0.5,  0. ,  0.5,  0. ,  0.5])
>>> hist.sum()
2.4999999999999996
>>> np.sum(hist*np.diff(bin_edges))
1.0

版本1.11.0中的新功能。

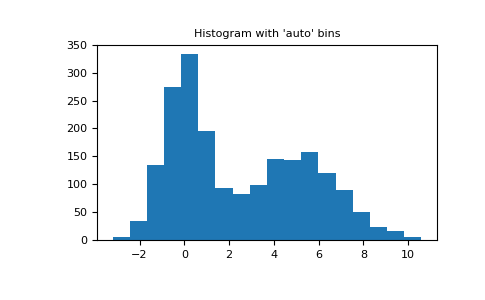
自动仓选择方法示例，使用2个具有2000点的峰值随机数据：

>>> import matplotlib.pyplot as plt
>>> rng = np.random.RandomState(10)  # deterministic random data
>>> a = np.hstack((rng.normal(size=1000),
...                rng.normal(loc=5, scale=2, size=1000)))
>>> plt.hist(a, bins='auto')  # plt.hist passes it's arguments to np.histogram
>>> plt.title("Histogram with 'auto' bins")
>>> plt.show()

（源代码，png，pdf）