使用RNN-RBM建模和生成复音音乐的序列¶
注意
本教程演示了如[BoulangerLewandowski12](pdf)中所述的RNN-RBM的基本实现。我们假设读者熟悉使用scan op和受限玻尔兹曼机(RBM)的循环神经网络。
注意
此部分的代码可从这里下载:rnnrbm.py。
您将需要在$PYTHONPATH中或工作目录中修改Python MIDI包(GPL许可证),以便将MIDI文件转换为钢琴卷轴和从钢琴卷轴转换。该脚本还假设../data目录中已提取诺丁汉民俗数据库的内容。此处提供备用MIDI数据集。
请注意,通过运行../data目录中的download.sh脚本,可以自动设置上述两种依赖关系。
警告
需要Theano 0.6或更多最近。
RNN-RBM ¶
The RNN-RBM is an energy-based model for density estimation of temporal sequences, where the feature vector 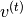 at time step
at time step 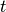 may be high-dimensional. 其允许通过一系列条件RBM(每个时间步长一个)描述
may be high-dimensional. 其允许通过一系列条件RBM(每个时间步长一个)描述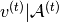 的多模态条件分布,其中
的多模态条件分布,其中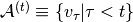 表示时间
表示时间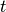 的序列历史,其参数
的序列历史,其参数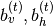 取决于具有隐藏单位
取决于具有隐藏单位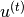 的确定性RNN的输出:
的确定性RNN的输出:
(1)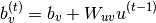
(2)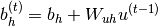
单层RNN复现关系定义为:
(3)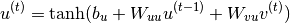
结果模型在下图中及时展开:
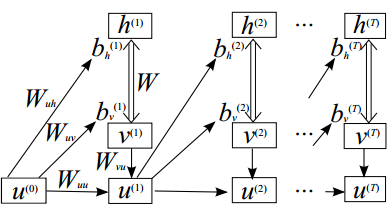
总概率分布由给定序列中的 时间步长上的和给出:
时间步长上的和给出:
(4)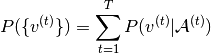
其中右侧被乘数是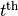 RBM的边缘化概率。
RBM的边缘化概率。
注意,为了实现的清楚,与[BoulangerLewandowski12]相反,我们使用对于权重矩阵的明显的命名约定,并且对于循环隐藏单元使用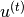 而不是
而不是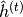 。
。
实现¶
我们希望构建两个Theano函数:一个用于训练RNN-RBM,一个用于从中生成样本序列。
对于训练,即给定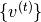 ,RNN隐藏状态
,RNN隐藏状态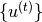 和相关联的
和相关联的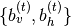 参数是确定性的,并且可以容易地为每个训练序列计算。然后可以通过对序列的各个时间步长的对比度发散(CD),以与在用于常规RBM的迷你批处理单个训练样本相同的方式来估计参数的随机梯度下降(SGD)更新。
参数是确定性的,并且可以容易地为每个训练序列计算。然后可以通过对序列的各个时间步长的对比度发散(CD),以与在用于常规RBM的迷你批处理单个训练样本相同的方式来估计参数的随机梯度下降(SGD)更新。
序列生成是类似的,除了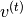 必须在每个时间步骤使用单独的(非批次)Gibbs链顺序取样,然后传递到重复和序列历史。
必须在每个时间步骤使用单独的(非批次)Gibbs链顺序取样,然后传递到重复和序列历史。
RBM层¶
下面显示的build_rbm函数通过CD近似从输入小批量(二进制矩阵)构建Gibbs链。注意,它还支持非批处理情况下的单个帧(二进制向量)。
def build_rbm(v, W, bv, bh, k):
'''Construct a k-step Gibbs chain starting at v for an RBM.
v : Theano vector or matrix
If a matrix, multiple chains will be run in parallel (batch).
W : Theano matrix
Weight matrix of the RBM.
bv : Theano vector
Visible bias vector of the RBM.
bh : Theano vector
Hidden bias vector of the RBM.
k : scalar or Theano scalar
Length of the Gibbs chain.
Return a (v_sample, cost, monitor, updates) tuple:
v_sample : Theano vector or matrix with the same shape as `v`
Corresponds to the generated sample(s).
cost : Theano scalar
Expression whose gradient with respect to W, bv, bh is the CD-k
approximation to the log-likelihood of `v` (training example) under the
RBM. The cost is averaged in the batch case.
monitor: Theano scalar
Pseudo log-likelihood (also averaged in the batch case).
updates: dictionary of Theano variable -> Theano variable
The `updates` object returned by scan.'''
def gibbs_step(v):
mean_h = T.nnet.sigmoid(T.dot(v, W) + bh)
h = rng.binomial(size=mean_h.shape, n=1, p=mean_h,
dtype=theano.config.floatX)
mean_v = T.nnet.sigmoid(T.dot(h, W.T) + bv)
v = rng.binomial(size=mean_v.shape, n=1, p=mean_v,
dtype=theano.config.floatX)
return mean_v, v
chain, updates = theano.scan(lambda v: gibbs_step(v)[1], outputs_info=[v],
n_steps=k)
v_sample = chain[-1]
mean_v = gibbs_step(v_sample)[0]
monitor = T.xlogx.xlogy0(v, mean_v) + T.xlogx.xlogy0(1 - v, 1 - mean_v)
monitor = monitor.sum() / v.shape[0]
def free_energy(v):
return -(v * bv).sum() - T.log(1 + T.exp(T.dot(v, W) + bh)).sum()
cost = (free_energy(v) - free_energy(v_sample)) / v.shape[0]
return v_sample, cost, monitor, updates
RNN层¶
build_rnnrbm函数定义RNN循环关系以获得RBM参数;复现函数足够灵活以在给出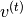 的训练场景中同时服务,并且在整个序列上一次构造“批量”RBM,并且在采样
的训练场景中同时服务,并且在整个序列上一次构造“批量”RBM,并且在采样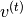 的生成场景中在每个时间步骤使用上面定义的Gibbs链分开。
的生成场景中在每个时间步骤使用上面定义的Gibbs链分开。
def build_rnnrbm(n_visible, n_hidden, n_hidden_recurrent):
'''Construct a symbolic RNN-RBM and initialize parameters.
n_visible : integer
Number of visible units.
n_hidden : integer
Number of hidden units of the conditional RBMs.
n_hidden_recurrent : integer
Number of hidden units of the RNN.
Return a (v, v_sample, cost, monitor, params, updates_train, v_t,
updates_generate) tuple:
v : Theano matrix
Symbolic variable holding an input sequence (used during training)
v_sample : Theano matrix
Symbolic variable holding the negative particles for CD log-likelihood
gradient estimation (used during training)
cost : Theano scalar
Expression whose gradient (considering v_sample constant) corresponds
to the LL gradient of the RNN-RBM (used during training)
monitor : Theano scalar
Frame-level pseudo-likelihood (useful for monitoring during training)
params : tuple of Theano shared variables
The parameters of the model to be optimized during training.
updates_train : dictionary of Theano variable -> Theano variable
Update object that should be passed to theano.function when compiling
the training function.
v_t : Theano matrix
Symbolic variable holding a generated sequence (used during sampling)
updates_generate : dictionary of Theano variable -> Theano variable
Update object that should be passed to theano.function when compiling
the generation function.'''
W = shared_normal(n_visible, n_hidden, 0.01)
bv = shared_zeros(n_visible)
bh = shared_zeros(n_hidden)
Wuh = shared_normal(n_hidden_recurrent, n_hidden, 0.0001)
Wuv = shared_normal(n_hidden_recurrent, n_visible, 0.0001)
Wvu = shared_normal(n_visible, n_hidden_recurrent, 0.0001)
Wuu = shared_normal(n_hidden_recurrent, n_hidden_recurrent, 0.0001)
bu = shared_zeros(n_hidden_recurrent)
params = W, bv, bh, Wuh, Wuv, Wvu, Wuu, bu # learned parameters as shared
# variables
v = T.matrix() # a training sequence
u0 = T.zeros((n_hidden_recurrent,)) # initial value for the RNN hidden
# units
# If `v_t` is given, deterministic recurrence to compute the variable
# biases bv_t, bh_t at each time step. If `v_t` is None, same recurrence
# but with a separate Gibbs chain at each time step to sample (generate)
# from the RNN-RBM. The resulting sample v_t is returned in order to be
# passed down to the sequence history.
def recurrence(v_t, u_tm1):
bv_t = bv + T.dot(u_tm1, Wuv)
bh_t = bh + T.dot(u_tm1, Wuh)
generate = v_t is None
if generate:
v_t, _, _, updates = build_rbm(T.zeros((n_visible,)), W, bv_t,
bh_t, k=25)
u_t = T.tanh(bu + T.dot(v_t, Wvu) + T.dot(u_tm1, Wuu))
return ([v_t, u_t], updates) if generate else [u_t, bv_t, bh_t]
# For training, the deterministic recurrence is used to compute all the
# {bv_t, bh_t, 1 <= t <= T} given v. Conditional RBMs can then be trained
# in batches using those parameters.
(u_t, bv_t, bh_t), updates_train = theano.scan(
lambda v_t, u_tm1, *_: recurrence(v_t, u_tm1),
sequences=v, outputs_info=[u0, None, None], non_sequences=params)
v_sample, cost, monitor, updates_rbm = build_rbm(v, W, bv_t[:], bh_t[:],
k=15)
updates_train.update(updates_rbm)
# symbolic loop for sequence generation
(v_t, u_t), updates_generate = theano.scan(
lambda u_tm1, *_: recurrence(None, u_tm1),
outputs_info=[None, u0], non_sequences=params, n_steps=200)
return (v, v_sample, cost, monitor, params, updates_train, v_t,
updates_generate)
将它们放在一起¶
我们现在拥有所有必要的成分,开始训练我们的网络对真实的符号序列的复调音乐。
class RnnRbm:
'''Simple class to train an RNN-RBM from MIDI files and to generate sample
sequences.'''
def __init__(
self,
n_hidden=150,
n_hidden_recurrent=100,
lr=0.001,
r=(21, 109),
dt=0.3
):
'''Constructs and compiles Theano functions for training and sequence
generation.
n_hidden : integer
Number of hidden units of the conditional RBMs.
n_hidden_recurrent : integer
Number of hidden units of the RNN.
lr : float
Learning rate
r : (integer, integer) tuple
Specifies the pitch range of the piano-roll in MIDI note numbers,
including r[0] but not r[1], such that r[1]-r[0] is the number of
visible units of the RBM at a given time step. The default (21,
109) corresponds to the full range of piano (88 notes).
dt : float
Sampling period when converting the MIDI files into piano-rolls, or
equivalently the time difference between consecutive time steps.'''
self.r = r
self.dt = dt
(v, v_sample, cost, monitor, params, updates_train, v_t,
updates_generate) = build_rnnrbm(
r[1] - r[0],
n_hidden,
n_hidden_recurrent
)
gradient = T.grad(cost, params, consider_constant=[v_sample])
updates_train.update(
((p, p - lr * g) for p, g in zip(params, gradient))
)
self.train_function = theano.function(
[v],
monitor,
updates=updates_train
)
self.generate_function = theano.function(
[],
v_t,
updates=updates_generate
)
def train(self, files, batch_size=100, num_epochs=200):
'''Train the RNN-RBM via stochastic gradient descent (SGD) using MIDI
files converted to piano-rolls.
files : list of strings
List of MIDI files that will be loaded as piano-rolls for training.
batch_size : integer
Training sequences will be split into subsequences of at most this
size before applying the SGD updates.
num_epochs : integer
Number of epochs (pass over the training set) performed. The user
can safely interrupt training with Ctrl+C at any time.'''
assert len(files) > 0, 'Training set is empty!' \
' (did you download the data files?)'
dataset = [midiread(f, self.r,
self.dt).piano_roll.astype(theano.config.floatX)
for f in files]
try:
for epoch in range(num_epochs):
numpy.random.shuffle(dataset)
costs = []
for s, sequence in enumerate(dataset):
for i in range(0, len(sequence), batch_size):
cost = self.train_function(sequence[i:i + batch_size])
costs.append(cost)
print('Epoch %i/%i' % (epoch + 1, num_epochs))
print(numpy.mean(costs))
sys.stdout.flush()
except KeyboardInterrupt:
print('Interrupted by user.')
def generate(self, filename, show=True):
'''Generate a sample sequence, plot the resulting piano-roll and save
it as a MIDI file.
filename : string
A MIDI file will be created at this location.
show : boolean
If True, a piano-roll of the generated sequence will be shown.'''
piano_roll = self.generate_function()
midiwrite(filename, piano_roll, self.r, self.dt)
if show:
extent = (0, self.dt * len(piano_roll)) + self.r
pylab.figure()
pylab.imshow(piano_roll.T, origin='lower', aspect='auto',
interpolation='nearest', cmap=pylab.cm.gray_r,
extent=extent)
pylab.xlabel('time (s)')
pylab.ylabel('MIDI note number')
pylab.title('generated piano-roll')
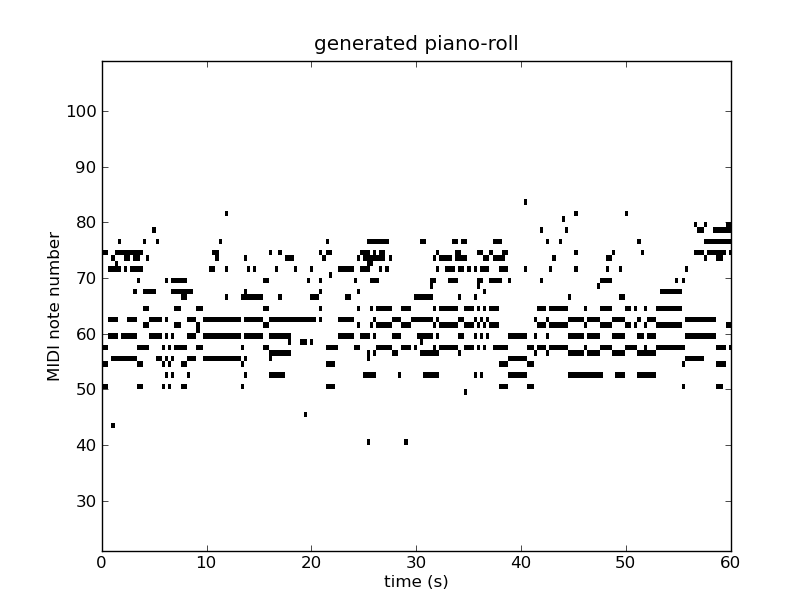
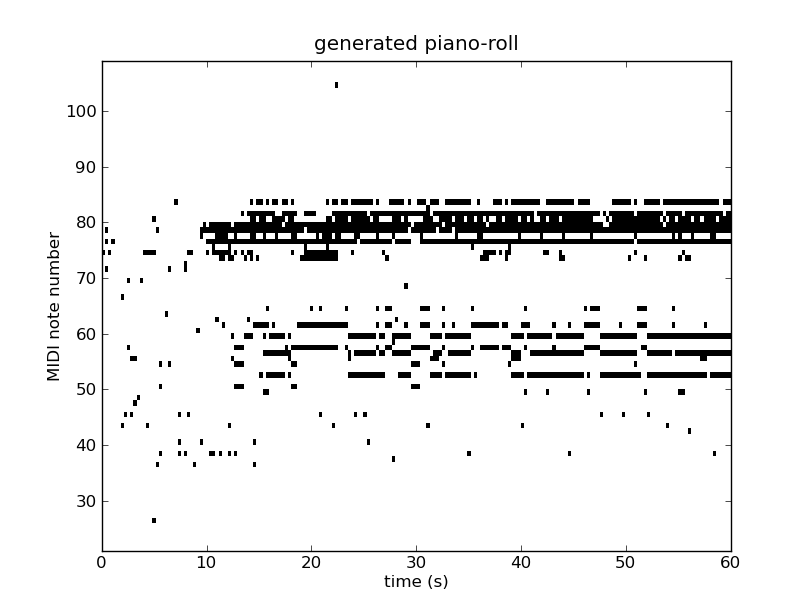
结果¶
我们在诺丁汉数据库上运行200个时代的代码;训练约需24小时。
输出如下:
Epoch 1/200 -15.0308940028
Epoch 2/200 -10.4892606673
Epoch 3/200 -10.2394696138
Epoch 4/200 -10.1431669994
Epoch 5/200 -9.7005382843
Epoch 6/200 -8.5985647524
Epoch 7/200 -8.35115428534
Epoch 8/200 -8.26453580552
Epoch 9/200 -8.21208991542
Epoch 10/200 -8.16847274143
... truncated for brevity ...
Epoch 190/200 -4.74799179994
Epoch 191/200 -4.73488515216
Epoch 192/200 -4.7326138489
Epoch 193/200 -4.73841636884
Epoch 194/200 -4.70255511452
Epoch 195/200 -4.71872634914
Epoch 196/200 -4.7276415885
Epoch 197/200 -4.73497644728
Epoch 198/200 -inf
Epoch 199/200 -4.75554987143
Epoch 200/200 -4.72591935412
下图显示了两个示例序列的钢琴卷,我们提供相应的MIDI文件:
如何改进此代码¶
本教程中显示的代码是一个精简版本,可以通过以下方式进行改进:
- 预处理:在公共音调(例如C大调/小调)中转置序列并且使每分钟的节拍(四分之一)的速度标准化可以对模型的生成质量具有最大影响。
- 预训练:用具有完全混洗帧(即,
 )的独立RBM初始化
)的独立RBM初始化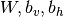 参数;使用辅助交叉熵目标通过SGD或优选地,无Hessian优化[BoulangerLewandowski12]来初始化RNN的
参数;使用辅助交叉熵目标通过SGD或优选地,无Hessian优化[BoulangerLewandowski12]来初始化RNN的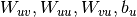 参数。
参数。 - 优化技术:梯度限幅,Nesterov动量和使用NADE条件密度估计。
- 超参数搜索:学习率(RBM和RNN部分分别),学习率计划,批量大小,隐藏单位数(循环和RBM),动量系数,动量计划,吉布斯链长
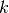 和早期停止。
和早期停止。 - 将初始条件
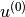 作为模型参数。
作为模型参数。
使用包含这些功能的代码生成的几个示例可在此处获取:sequences.zip。