numpy.random.normal¶

numpy.random.normal(loc=0.0, scale=1.0, size=None)¶

从正态（高斯）分布绘制随机样本。

正态分布的概率密度函数，首先由De Moivre推导，200年后由高斯和拉普拉斯独立地[R250]导出，通常称为钟形曲线，因为其特征形状下面）。

正态分布本质上经常发生。例如，它描述了受大量微小随机干扰影响的样本的常见分布，每种干扰具有其自身的独特分布[R250]。

参数：	loc：float 平均值（“中心”）的分布。 scale：float 分布的标准偏差（展布或“宽度”）。 size：int或tuple的整数，可选输出形状。如果给定形状是例如`（m， n， k）`，则 `m * n * k`默认值为None，在这种情况下返回单个值。

也可以看看

scipy.stats.distributions.norm: 概率密度函数，分布或累积密度函数等。

笔记

高斯分布的概率密度为

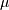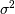其中 $\mu$ 是平均值， $\sigma$ 标准偏差。标准偏差的平方， $\sigma^2$ ，称为方差。

该函数在平均值处具有峰值，其“扩展”随标准偏差（在 $x + \sigma$ 和 $x - \sigma$ [R250]时达到其最大值的0.607倍）。这意味着numpy.random.normal更可能返回接近平均值的样本，而不是那些远离平均值的样本。

参考文献

[R249]

维基百科，“正态分布”，http://en.wikipedia.org/wiki/Normal_distribution

[R250]

（1，2，3，4） PR Peebles Jr.， Central Limit Theorem“in”Probability，Random Variables and Random Signal Principles“，4th ed。，2001，pp。51，51，125。

例子

从分布绘制样本：

>>> mu, sigma = 0, 0.1 # mean and standard deviation
>>> s = np.random.normal(mu, sigma, 1000)

验证平均值和方差：

>>> abs(mu - np.mean(s)) < 0.01
True

>>> abs(sigma - np.std(s, ddof=1)) < 0.01
True

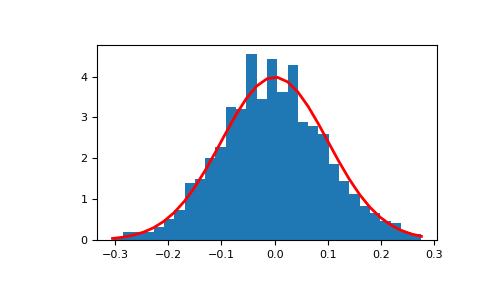
显示样本的直方图，以及概率密度函数：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 30, normed=True)
>>> plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
...                np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
...          linewidth=2, color='r')
>>> plt.show()

（源代码，png，pdf）