numpy.random.multivariate_normal¶
-
numpy.random.multivariate_normal(mean, cov[, size])¶ 从多变量正态分布绘制随机样本。
多元正态,多正态或高斯分布是一维正态分布到更高维度的泛化。这样的分布由其平均和协方差矩阵指定。这些参数类似于一维正态分布的平均值(平均或“中心”)和方差(标准偏差,或“宽度”,平方)。
参数: 表示:1-D array_like,长度为N
N维分布的均值。
cov:2-D array_like,形状(N,N)
分布的协方差矩阵。它必须是对称和正半定的正确采样。
size:int或tuple的整数,可选
给定例如
(m,n,k),m*n*k个样本的形状,并且在m t4 > -t n -by- k排列。因为每个样本是N t0维,所以输出形状是(m,n,k,N)。如果未指定形状,则返回单个(N -D)样本。返回: out:ndarray
绘制的样本,如果提供的话,形状大小。如果不是,则形状为
(N,)。换句话说,每个条目
out[i,j,...,:]是从分布绘制的N维值。笔记
平均值是N维空间中的坐标,其表示样本最可能被生成的位置。这类似于一维或单变量正态分布的钟形曲线的峰值。
协方差表示两个变量一起变化的水平。从多变量正态分布,我们绘制N维样本,
![X = [x_1, x_2, ... x_N]](../../_images/math/5207fbc5c81de717782578cb4156d60d83c10a94.png) 。协方差矩阵元素
。协方差矩阵元素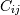 是
是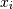 和
和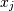 的协方差。元素
的协方差。元素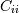 是
是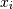 的方差(即其“扩展”)。
的方差(即其“扩展”)。代替指定完全协方差矩阵,流行的近似包括:
- 球面协方差(cov是单位矩阵的倍数)
- 对角协方差(cov具有非负元素,仅在对角线上)
通过绘制生成的数据点,可以在二维中看到该几何属性:
>>> mean = [0, 0] >>> cov = [[1, 0], [0, 100]] # diagonal covariance
对角协方差意味着点沿x或y轴取向:
>>> import matplotlib.pyplot as plt >>> x, y = np.random.multivariate_normal(mean, cov, 5000).T >>> plt.plot(x, y, 'x') >>> plt.axis('equal') >>> plt.show()
注意协方差矩阵必须是正半定的(a.k.a.非负定义)。否则,此方法的行为未定义,不能保证向后兼容性。
参考文献
[R241] Papoulis,A.,“Probability,Random Variables,and Stochastic Processes,”3rd ed。,New York:McGraw-Hill,1991。 [R242] Duda,R.O.,Hart,P.E.,and Stork,D.G。,“Pattern Classification,”2nd ed。,New York:Wiley,2001。 例子
>>> mean = (1, 2) >>> cov = [[1, 0], [0, 1]] >>> x = np.random.multivariate_normal(mean, cov, (3, 3)) >>> x.shape (3, 3, 2)
以下是可能是真的,因为0.6大约是标准偏差的两倍:
>>> list((x[0,0,:] - mean) < 0.6) [True, True]