numpy.random.RandomState.zipf

RandomState.zipf(a, size=None)

从Zipf分布绘制样本。

样本从具有指定参数a> 1的Zipf分布中绘制。

Zipf分布（也称为zeta分布）是满足Zipf定律的连续概率分布：项目的频率与其在频率表中的秩成反比。

参数：

a：float> 1

分布参数。

size：int或tuple的整数，可选

输出形状。如果给定形状是例如（m， n， k），则 m * n * k默认值为None，在这种情况下返回单个值。

返回：

samples：scalar或ndarray

返回的样本大于或等于1。

也可以看看

scipy.stats.distributions.zipf

概率密度函数，分布或累积密度函数等。

笔记

Zipf分布的概率密度为

其中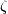是Riemann Zeta函数。

它以美国语言学家乔治·金斯利·齐普（George Kingsley Zipf）的名字命名，他指出语言样本中任何单词的频率与其在频率表中的排名成反比。

参考文献

[R207]

Zipf，G.K.，“Selected Studies of the Principle of Relative Frequency in Language”，Cambridge，MA：Harvard Univ。Press，1932。

例子

从分布绘制样本：

>>> a = 2. # parameter
>>> s = np.random.zipf(a, 1000)

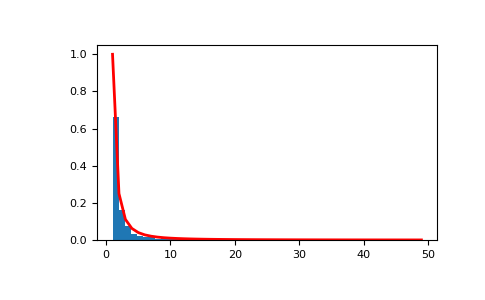
显示样本的直方图，以及概率密度函数：

>>> import matplotlib.pyplot as plt
>>> import scipy.special as sps
Truncate s values at 50 so plot is interesting
>>> count, bins, ignored = plt.hist(s[s<50], 50, normed=True)
>>> x = np.arange(1., 50.)
>>> y = x**(-a)/sps.zetac(a)
>>> plt.plot(x, y/max(y), linewidth=2, color='r')
>>> plt.show()

（源代码，png，pdf）