numpy.random.RandomState.binomial¶
-
RandomState.binomial(n, p, size=None)¶ 从二项分布绘制样本。
样本从具有指定参数,n个试验和p成功概率的二项分布中得到,其中n是> = 0的整数,并且p在区间[0,1]中。(n可以作为float输入,但在使用中被截断为整数)
参数: n:float(但截断为整数)
参数,> = 0。
p:float
参数,> = 0和
size:int或tuple的整数,可选
输出形状。如果给定形状是例如
(m, n, k),则m * n * k默认值为None,在这种情况下返回单个值。返回: samples:ndarray或scalar
其中值是[0,n]中的所有整数。
也可以看看
scipy.stats.distributions.binom- 概率密度函数,分布或累积密度函数等。
笔记
二项分布的概率密度为
其中
 是试验次数,
是试验次数,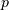 是成功的概率,
是成功的概率,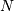 是成功次数。
是成功次数。当通过使用随机样本估计群体中的比例的标准误差时,正态分布工作良好,除非产物p * n例如,15个人的样本显示4个左手,11个右手。然后p = 4/15 = 27%。0.27 * 15 = 4,因此在这种情况下应使用二项分布。
参考文献
[R137] Dalgaard,Peter,“Introductory Statistics with R”,Springer-Verlag,2002。 [R138] Glantz,Stanton A.“Primer of Biostatistics。”,McGraw-Hill,第五版,2002。 [R139] Lentner,Marvin,“Elementary Applied Statistics”,Bogden和Quigley,1972。 [R140] Weisstein,Eric W.“二项分布”,来自MathWorld-Wolfram Web资源。http://mathworld.wolfram.com/BinomialDistribution.html [R141] 维基百科,“二项分布”,http://en.wikipedia.org/wiki/Binomial_distribution 例子
从分布绘制样本:
>>> n, p = 10, .5 # number of trials, probability of each trial >>> s = np.random.binomial(n, p, 1000) # result of flipping a coin 10 times, tested 1000 times.
一个现实世界的例子。一家公司钻探9个野生猫油勘探井,每个井的估计成功概率为0.1。所有九口井都失败了。发生这种情况的概率是多少?
让我们做模型的20,000个试验,并计数产生零个阳性结果的数量。
>>> sum(np.random.binomial(9, 0.1, 20000) == 0)/20000. # answer = 0.38885, or 38%.