numpy.polynomial.chebyshev.chebint

numpy.polynomial.chebyshev.chebint(c, m=1, k=[], lbnd=0, scl=1, axis=0)

集成Chebyshev系列。

返回沿轴从lbnd积分m次的切比雪夫系数c。在每次迭代中，通过scl将所得到的系列相乘，并且添加积分常数k。缩放因子用于变量的线性变化。（“买方谨慎”：请注意，根据所做的操作，可能希望scl是所期望的倒数；有关详细信息，请参阅下面的“注释”部分。The argument c is an array of coefficients from low to high degree along each axis, e.g., [1,2,3] represents the series T_0 + 2*T_1 + 3*T_2 while [[1,2],[1,2]] represents 1*T_0(x)*T_0(y) + 1*T_1(x)*T_0(y) + 2*T_0(x)*T_1(y) + 2*T_1(x)*T_1(y) if axis=0 is x and axis=1 is y.

参数：

c：array_like

切比雪夫系数系数。如果c是多维的，则不同的轴对应于不同的变量，每个轴中的度由相应的索引给出。

m：int，可选

整合顺序，必须是积极的。（默认值：1）

k：{[]，list，scalar}，可选

积分常数。在零处的第一积分的值是列表中的第一值，在零处的第二积分的值是第二值等。如果k == []（默认值），所有常数都设置为零。如果m == 1，可以给出单个标量而不是列表。

lbnd：标量，可选

积分的下限。（默认值：0）

scl：标量，可选

Following each integration the result is multiplied by scl before the integration constant is added. （默认值：1）

axis：int，可选

进行积分的轴。（默认值：0）。

版本1.7.0中的新功能。

返回：

S：ndarray

C系数积分的系数。

上升：

ValueError

如果m 1，len（k） ＆gt； m，np.isscalar（lbnd） == / t11>或np.isscalar（scl） == False。

也可以看看

chebder

笔记

请注意，每次积分的结果乘乘以scl。为什么这一点很重要？假设变量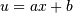在相对于x的积分中进行线性变化。然后.. math :: dx = du / a，因此需要设置scl等于 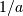- 也许不是一开始就想到的。

还要注意，一般来说，集成C系列的结果需要“重新投射”到C系列基本集上。因此，通常，该函数的结果是“不直观的”，虽然正确；请参阅下面的示例部分。

例子

>>> from numpy.polynomial import chebyshev as C
>>> c = (1,2,3)
>>> C.chebint(c)
array([ 0.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,3)
array([ 0.03125   , -0.1875    ,  0.04166667, -0.05208333,  0.01041667,
        0.00625   ])
>>> C.chebint(c, k=3)
array([ 3.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,lbnd=-2)
array([ 8.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,scl=-2)
array([-1.,  1., -1., -1.])