numpy.linalg.pinv¶
-
numpy.linalg.pinv(a, rcond=1e-15)[source]¶ 计算矩阵的(Moore-Penrose)伪逆。
使用奇异值分解(SVD)并包括所有大奇异值计算矩阵的广义逆。
参数: a:(M,N)array_like
要进行伪反转的矩阵。
rcond:float
小奇异值的截止值。比rcond * highest_singular_value(再次,以模数)更小的(模数)奇异值被设置为零。
返回: B:(N,M)ndarray
a的伪逆。如果a是矩阵实例,则B。
上升: LinAlgError
如果SVD计算不收敛。
笔记
表示为
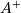 的矩阵A的伪逆定义为:“求解'[最小二乘问题]
的矩阵A的伪逆定义为:“求解'[最小二乘问题] 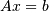 的矩阵,即,如果
的矩阵,即,如果 是所述解,那么
是所述解,那么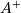 是
是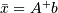 的矩阵。
的矩阵。可以表明,如果
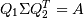 是A的奇异值分解,则
是A的奇异值分解,则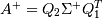 ,其中
,其中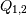 是正交矩阵,
是正交矩阵,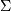 是由A的所谓奇异值组成的对角矩阵, (通常由零),然后
是由A的所谓奇异值组成的对角矩阵, (通常由零),然后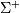 仅仅是由A的奇异值的倒数(再次,之后是零)组成的对角矩阵。[R42]
仅仅是由A的奇异值的倒数(再次,之后是零)组成的对角矩阵。[R42]参考文献
[R42] (1,2) G. Strang,线性代数及其应用,第2版,Orlando,FL ,Academic Press,Inc.,1980,pp。139-142。 例子
The following example checks that
a * a+ * a == aanda+ * a * a+ == a+:>>> a = np.random.randn(9, 6) >>> B = np.linalg.pinv(a) >>> np.allclose(a, np.dot(a, np.dot(B, a))) True >>> np.allclose(B, np.dot(B, np.dot(a, B))) True