numpy.linalg.cholesky¶

numpy.linalg.cholesky(a)[source]¶

Cholesky分解。

返回方矩阵a的Cholesky分解L * LH，其中L是下三角形，而H是共轭转置运算符（如果a是实数值，则是普通转置）。a必须是Hermitian（如果实数值对称的）和正定数。只有L实际返回。

参数：	a：（...，M，M）array_like Hermitian（如果所有元素都是实数，则为对称），正定输入矩阵。
返回：	L：（...，M，M）array_like 上或下三角形Cholesky因子a。如果a是一个矩阵对象，则返回一个矩阵对象。
上升：	LinAlgError 如果分解失败，例如，如果a不是正定的。

参数：

a：（...，M，M）array_like

Hermitian（如果所有元素都是实数，则为对称），正定输入矩阵。

L：（...，M，M）array_like

上或下三角形Cholesky因子a。如果a是一个矩阵对象，则返回一个矩阵对象。

上升：

LinAlgError

如果分解失败，例如，如果a不是正定的。

笔记

版本1.8.0中的新功能。

广播规则适用，有关详细信息，请参阅numpy.linalg文档。

Cholesky分解经常被用作一种快速的求解方法

（当A是厄米/对称和正定时）。

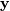
首先，我们解决 $\mathbf{y}$

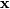
然后为 $\mathbf{x}$

例子

>>> A = np.array([[1,-2j],[2j,5]])
>>> A
array([[ 1.+0.j,  0.-2.j],
       [ 0.+2.j,  5.+0.j]])
>>> L = np.linalg.cholesky(A)
>>> L
array([[ 1.+0.j,  0.+0.j],
       [ 0.+2.j,  1.+0.j]])
>>> np.dot(L, L.T.conj()) # verify that L * L.H = A
array([[ 1.+0.j,  0.-2.j],
       [ 0.+2.j,  5.+0.j]])
>>> A = [[1,-2j],[2j,5]] # what happens if A is only array_like?
>>> np.linalg.cholesky(A) # an ndarray object is returned
array([[ 1.+0.j,  0.+0.j],
       [ 0.+2.j,  1.+0.j]])
>>> # But a matrix object is returned if A is a matrix object
>>> LA.cholesky(np.matrix(A))
matrix([[ 1.+0.j,  0.+0.j],
        [ 0.+2.j,  1.+0.j]])