numpy.polynomial.polynomial.polyfromroots

numpy.polynomial.polynomial.polyfromroots(roots)

生成具有给定根的monic多项式。

返回多项式的系数

其中r_n是在根中指定的根。如果零具有多重性n，则它必须出现在根中n次。例如，如果2是多重性三的根，3是多重性2的根，则根看起来像[2,2,2,3,3]。根可以以任何顺序出现。

如果返回的系数是c，则

这种形式的单项多项式的最后一项的系数为1。

参数：

根：array_like

包含根的序列。

返回：

out：ndarray

多项式系数的1-D数组如果所有根都是实数，则out也是实数，否则是复数。（参见下文实施例）。

也可以看看

chebfromroots，legfromroots，lagfromroots，hermfromroots，hermefromroots

笔记

通过将形式（x-r_i）的线性因子相乘来确定系数，即

其中n == len（root） - 1 t0>；请注意，这意味着总是返回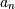的1。

例子

>>> from numpy.polynomial import polynomial as P
>>> P.polyfromroots((-1,0,1)) # x(x - 1)(x + 1) = x^3 - x
array([ 0., -1.,  0.,  1.])
>>> j = complex(0,1)
>>> P.polyfromroots((-j,j)) # complex returned, though values are real
array([ 1.+0.j,  0.+0.j,  1.+0.j])