numpy.polynomial.polynomial.polyfit¶

numpy.polynomial.polynomial.polyfit(x, y, deg, rcond=None, full=False, w=None)[source]¶

多项式与数据的最小二乘拟合。

返回度为deg的多项式的系数，其是在点x给出的数据值y的最小二乘拟合。如果y是1-D，则返回的系数也将是1-D。如果y是2-D多重拟合，对于y的每一列进行一次，并且所得到的系数存储在2-D返回的相应列中。拟合的多项式是形式

其中n是deg。

参数：	x：array_like，shape（M） M u>样本（数据）点`（x [i]， y [i]）。` y：array_like，shape（M）或（M，K y坐标。通过传递y包含一个数据的2-D数组，可共享相同x坐标的几组采样点可以（独立地）适应一次对`polyfit`的调用每列设置。 deg：int或1-D array_like 拟合多项式的度（s）。如果deg是单个整数，则包括deg项的所有项包括在拟合中。对于Numpy版本> = 1.11，可以使用指定要包括的术语的度数的整数列表。 rcond：float，可选相对条件编号。小于rcond的奇异值相对于最大奇异值将被忽略。默认值为`len(x)eps`，其中eps是平台浮点类型的相对精度，在大多数情况下约为2e-16。 full：bool，可选开关确定返回值的性质。当`False`（默认）只返回系数；当`True`时，也返回来自奇异值分解（用于求解拟合矩阵方程）的诊断信息。 w：array_like，shape（M，），可选重量。如果不是无，则通过w [i]加权每个点`(x[i],y[i])`对拟合的贡献。理想地，选择权重使得乘积`w[i]y[i]`的误差都具有相同的方差。默认值为“无”。版本1.5.0中的新功能。
返回：	coef：ndarray，shape（deg + 1，）或（deg + 1，K 多项式系数从低到高排序。如果y是2-D，则coef的列k中的系数表示在y t3中的数据的多项式拟合>'t k列。 [residuals，rank，singular_values，rcond]：list 只有full = True时，才会返回这些值 resid – sum of squared residuals of the least squares fit rank – the numerical rank of the scaled Vandermonde matrix sv – singular values of the scaled Vandermonde matrix rcond – value of rcond. 有关详细信息，请参阅linalg.lstsq。
上升：	RankWarning 如果最小二乘拟合中的矩阵是秩不足，则引发。只有在满 == False时，才会发出警告。警告可以通过以下方式关闭： >>> import warnings >>> warnings.simplefilter('ignore', RankWarning)

参数：

x：array_like，shape（M）

M u>样本（数据）点（x [i]， y [i]）。

y：array_like，shape（M）或（M，K

y坐标。通过传递y包含一个数据的2-D数组，可共享相同x坐标的几组采样点可以（独立地）适应一次对polyfit的调用每列设置。

deg：int或1-D array_like

拟合多项式的度（s）。如果deg是单个整数，则包括deg项的所有项包括在拟合中。对于Numpy版本> = 1.11，可以使用指定要包括的术语的度数的整数列表。

rcond：float，可选

相对条件编号。小于rcond的奇异值相对于最大奇异值将被忽略。默认值为len(x)*eps，其中eps是平台浮点类型的相对精度，在大多数情况下约为2e-16。

full：bool，可选

开关确定返回值的性质。当False（默认）只返回系数；当True时，也返回来自奇异值分解（用于求解拟合矩阵方程）的诊断信息。

w：array_like，shape（M，），可选

重量。如果不是无，则通过w [i]加权每个点(x[i],y[i])对拟合的贡献。理想地，选择权重使得乘积w[i]*y[i]的误差都具有相同的方差。默认值为“无”。

版本1.5.0中的新功能。

coef：ndarray，shape（deg + 1，）或（deg + 1，K

多项式系数从低到高排序。如果y是2-D，则coef的列k中的系数表示在y t3中的数据的多项式拟合>'t k列。

[residuals，rank，singular_values，rcond]：list

只有full = True时，才会返回这些值

resid – sum of squared residuals of the least squares fit rank – the numerical rank of the scaled Vandermonde matrix sv – singular values of the scaled Vandermonde matrix rcond – value of rcond.

有关详细信息，请参阅linalg.lstsq。

上升：

RankWarning

如果最小二乘拟合中的矩阵是秩不足，则引发。只有在满 == False时，才会发出警告。警告可以通过以下方式关闭：
>>> import warnings
>>> warnings.simplefilter('ignore', RankWarning)

也可以看看

chebfit，legfit，lagfit，hermfit，hermefit

polyval: 评估多项式。
polyvander: 权力的范德蒙矩阵。
linalg.lstsq: 从矩阵计算最小二乘拟合。
scipy.interpolate.UnivariateSpline: 计算样条拟合。

笔记

解决方案是多项式p的系数，其使加权平方误差的和最小化

其中 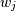$w_j$ 是权重。该问题通过设置（通常）过度确定的矩阵方程来解决：

其中V是x的加权伪Vandermonde矩阵，c是要求解的系数，w权重和y是观察值。然后使用V的奇异值分解来求解该方程。

如果V的一些奇异值如此小以至于它们被忽略（并且满 == False），则RankWarning 。这意味着可能不良地确定系数值。拟合一个低阶多项式通常会摆脱警告（但可能不是你想要的，当然；如果你有独立的理由选择不工作的程度，你可能必须：a）重新考虑这些原因，和/或b）重新考虑您的数据的质量。rcond参数也可以设置为小于其默认值的值，但是所得到的拟合可能是假的并且具有来自舍入误差的较大贡献。

使用双精度的多项式拟合在大约（多项式）度20处倾向于“失败”。使用Chebyshev或Legendre系列的拟合通常被更好地条件化，但很大程度上仍然可以取决于样本点的分布和数据的平滑性。如果配合的质量不足，花键可能是一个好的选择。

例子

>>> from numpy.polynomial import polynomial as P
>>> x = np.linspace(-1,1,51) # x "data": [-1, -0.96, ..., 0.96, 1]
>>> y = x**3 - x + np.random.randn(len(x)) # x^3 - x + N(0,1) "noise"
>>> c, stats = P.polyfit(x,y,3,full=True)
>>> c # c[0], c[2] should be approx. 0, c[1] approx. -1, c[3] approx. 1
array([ 0.01909725, -1.30598256, -0.00577963,  1.02644286])
>>> stats # note the large SSR, explaining the rather poor results
[array([ 38.06116253]), 4, array([ 1.38446749,  1.32119158,  0.50443316,
0.28853036]), 1.1324274851176597e-014]

同样的事情没有增加的噪音

>>> y = x**3 - x
>>> c, stats = P.polyfit(x,y,3,full=True)
>>> c # c[0], c[2] should be "very close to 0", c[1] ~= -1, c[3] ~= 1
array([ -1.73362882e-17,  -1.00000000e+00,  -2.67471909e-16,
         1.00000000e+00])
>>> stats # note the minuscule SSR
[array([  7.46346754e-31]), 4, array([ 1.38446749,  1.32119158,
0.50443316,  0.28853036]), 1.1324274851176597e-014]