numpy.convolve

numpy.convolve(a, v, mode='full')

返回两个一维序列的离散，线性卷积。

卷积算子常常出现在信号处理中，其中它模拟线性时不变系统对信号[R17]的影响。在概率理论中，两个独立的随机变量的和根据它们各自的分布的卷积来分布。

如果v长于a，则在计算之前交换数组。

参数：

a：（N，）array_like

第一维一维输入数组。

v：（M，）array_like

第二维一维输入数组。

mode：{'full'，'valid'，'same'}，可选

'充分'：

默认情况下，模式为“full”。这在每个重叠点处返回卷积，其输出形状为（N + M-1，）。在卷积的端点，信号不完全重叠，并且可以看到边界效应。

'相同'：

模式“相同”返回长度max（M， N）的输出。边界效应仍然可见。

'有效'：

模式'有效'返回长度max（M， N） - N） + 1。卷积积仅用于信号完全重叠的点。信号边界外的值没有效果。

返回：

out：ndarray

a和v的离散，线性卷积。

也可以看看

scipy.signal.fftconvolve

使用快速傅里叶变换卷积两个数组。

scipy.linalg.toeplitz

用于构造卷积运算符。

polymul

多项式乘法。与卷积相同的输出，但也接受poly1d对象作为输入。

笔记

离散卷积运算定义为

It can be shown that a convolution 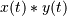in time/space is equivalent to the multiplication 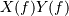in the Fourier domain, after appropriate padding (padding is necessary to prevent circular convolution). 由于乘法比卷积更有效（更快），函数scipy.signal.fftconvolve利用FFT来计算大数据集的卷积。

参考文献

[R17]

（1，2） Wikipedia，“Convolution”，http://en.wikipedia.org/wiki/Convolution 。

例子

注意卷积运算符如何在“滑动”两个数组之前翻转第二个数组：

>>> np.convolve([1, 2, 3], [0, 1, 0.5])
array([ 0. ,  1. ,  2.5,  4. ,  1.5])

只返回卷积的中间值。包含边界效应，其中考虑零：

>>> np.convolve([1,2,3],[0,1,0.5], 'same')
array([ 1. ,  2.5,  4. ])

两个数组具有相同的长度，因此只有一个位置，它们完全重叠：

>>> np.convolve([1,2,3],[0,1,0.5], 'valid')
array([ 2.5])